ASATriangle

ASATriangle[α,c,β]

returns a filled triangle with angles α and β and side length c, and c is adjacent to both angles.

Details and Options

  • ASATriangle is also known as angle-side-angle triangle.
  • ASATriangle can be used as a primitive in 2D graphics and as a geometric region in 2D.
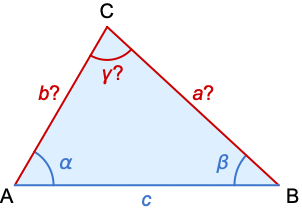
  • The given (blue) and computed (red) parameters for an ASATriangle:
  • ASATriangle returns a Triangle with 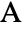at the origin, 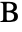on the positive 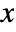axis, and 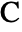in the half-plane .
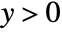  • ASATriangle allows the length c to be any positive number and the angles α and β to be positive and such that α+β<π.

Background & Context

  • ASATriangle constructs an angle-side-angle triangle. In particular, ASATriangle[α,c,β] represents the Triangle in TemplateBox[{}, Reals]^2 with vertices , and 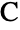located at the origin, on the positive 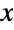axis and in the upper half-plane, respectively, with α∠BAC, β∠ABC and c the length of the side opposite 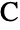. By the ASA theorem, the triangle so specified is unique (up to geometric congruence). ASATriangle allows the length c to be any positive number and the angles α and β to be positive values satisfying α+β<π. The arguments of ASATriangle may be exact or approximate numeric expressions.
  • The Triangle objects returned by ASATriangle can be used as 2D graphics primitives or geometric regions.
  • ASATriangle is related to a number of other symbols. AASTriangle, SASTriangle and SSSTriangle return two-dimensional triangles constructed using different angle and/or side specifications. ASATriangle is a special case of Triangle, in the sense that ASATriangle[α,c,β] is equivalent to Triangle[{{0,0},{c,0},{c x,c y}}] for xCos[α] Csc[α+β] Sin[β] and yCsc[α+β] Sin[α] Sin[β].

Examples

open allclose all

Basic Examples  (4)

A triangle with , , and :

An ASATriangle:

Different styles applied to ASATriangle:

Area and centroid:

Centroid:

Scope  (14)

Graphics  (4)

Specification  (2)

ASATriangle evaluates to Triangle with one point at the origin and one edge on the axis:

A triangle with a symbolic angle:

Plot them:

Styling  (2)

Color directives specify the face color:

FaceForm and EdgeForm can be used to specify the styles of the interior and boundary:

Regions  (10)

Embedding dimension is the dimension of the space in which the triangle lives:

Geometric dimension is the dimension of the triangle itself:

Membership testing:

Get conditions for membership:

Area:

Centroid:

Distance from a point to an ASATriangle:

Signed distance from a point:

Now plot it:

Nearest point:

Visualize it:

A triangle is bounded:

Find its range:

Integrate over an ASATriangle:

Optimize over it:

Solve equations over an ASATriangle:

Applications  (2)

A triangle with two equal angles is an isosceles triangle:

Visualize it:

Find its area:

The circumcircle of an ASATriangle can be found using Circumsphere:

The circumcircle passes through the three corner points:

Find the midpoints for each edge of the triangle:

The perpendicular bisectors are lines from the circumcenter to the midpoints:

Properties & Relations  (2)

ASATriangle is a specialized case of Triangle:

Any ASATriangle can be represented by a Polygon:

Neat Examples  (1)

Varying two angles together:

Wolfram Research (2014), ASATriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/ASATriangle.html.

Text

Wolfram Research (2014), ASATriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/ASATriangle.html.

CMS

Wolfram Language. 2014. "ASATriangle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ASATriangle.html.

APA

Wolfram Language. (2014). ASATriangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ASATriangle.html

BibTeX

@misc{reference.wolfram_2024_asatriangle, author="Wolfram Research", title="{ASATriangle}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ASATriangle.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_asatriangle, organization={Wolfram Research}, title={ASATriangle}, year={2014}, url={https://reference.wolfram.com/language/ref/ASATriangle.html}, note=[Accessed: 21-November-2024 ]}