SSSTriangle

SSSTriangle[a,b,c]

returns a filled triangle with sides of lengths a, b, and c.

Details and Options

  • SSSTriangle is also known as side-side-side triangle.
  • SSSTriangle can be used as a primitive in 2D graphics and as a geometric region in 2D.
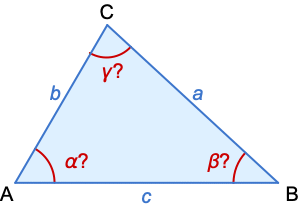
  • The given (blue) and computed (red) parameters for an SSSTriangle:
  • SSSTriangle returns a Triangle with A at the origin, B on the positive 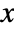axis, and C in the half-plane .
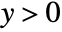  • SSSTriangle allows the lengths a, b, and c to be any positive numbers such that each of them is less than the sum of the other two.

Background & Context

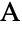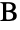  • SSSTriangle constructs a side-side-side triangle. In particular, SSSTriangle[a,b,c] returns the Triangle in TemplateBox[{}, Reals]^2 with vertices , and 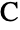located at the origin, on the positive 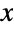axis and in the upper half-plane, respectively, with a, b and c the lengths of the sides opposite vertices 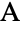, 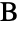and 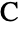. By the SSS theorem, the triangle so specified is unique (up to geometric congruence). The arguments of SSSTriangle may be any positive numbers (exact or approximate) such that each is less than the sum of the other two (i.e. such that the triangle inequality is satisfied).
  • The Triangle objects returned by SSSTriangle can be used as 2D graphics primitives or geometric regions.
  • SSSTriangle is related to a number of other symbols. AASTriangle, ASATriangle and SASTriangle return two-dimensional triangles constructed using different angle and/or side specifications. Finally, SSSTriangle is a special case of Triangle, in the sense that SSSTriangle[a,b,c] is equivalent to Triangle[{{0,0},{c,0},{y,z}}] for y(-a^2+b^2+c^2)/(2 c) and z==Sqrt[(a+b-c)(a-b+c) (-a+b+c) (a+b+c)]/(2 c).

Examples

open allclose all

Basic Examples  (4)

A triangle with , , and :

An SSSTriangle:

Different styles applied to SSSTriangle:

Area and centroid:

Centroid:

Scope  (14)

Graphics  (4)

Specification  (2)

SSSTriangle evaluates to Triangle with one point at the origin and one edge on the axis:

A triangle with symbolic lengths:

Plot them:

Styling  (2)

Color directives specify the face color:

FaceForm and EdgeForm can be used to specify the styles of the interior and boundary:

Regions  (10)

Embedding dimension is the dimension of the space in which the triangle lives:

Geometric dimension is the dimension of the shape itself:

Membership testing:

Conditions for membership:

Area:

Centroid:

Distance from a point to an SSSTriangle:

Plot it:

Signed distance from a point:

Now plot it:

Nearest point:

Visualize it:

A triangle is bounded:

The bounding range:

Integrate over an SSSTriangle:

Optimize over it:

Solve equations over an SSSTriangle:

Applications  (3)

A triangle in which all sides are equal is an equilateral triangle:

Visualize it:

Find its area:

The circumcircle of an SSSTriangle can be found using Circumsphere:

The circumcircle passes through the three corner points:

Find the midpoints for each edge of the triangle:

The perpendicular bisectors are lines from the circumcenter to the midpoints:

Minimize the perimeter of an SSSTriangle with fixed area:

As expected, the result is an equilateral triangle:

Properties & Relations  (2)

SSSTriangle is a specialized case of Triangle:

Any SSSTriangle can be represented by a Polygon:

Neat Examples  (1)

Varying one side length:

Wolfram Research (2014), SSSTriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/SSSTriangle.html.

Text

Wolfram Research (2014), SSSTriangle, Wolfram Language function, https://reference.wolfram.com/language/ref/SSSTriangle.html.

CMS

Wolfram Language. 2014. "SSSTriangle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SSSTriangle.html.

APA

Wolfram Language. (2014). SSSTriangle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SSSTriangle.html

BibTeX

@misc{reference.wolfram_2024_ssstriangle, author="Wolfram Research", title="{SSSTriangle}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SSSTriangle.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ssstriangle, organization={Wolfram Research}, title={SSSTriangle}, year={2014}, url={https://reference.wolfram.com/language/ref/SSSTriangle.html}, note=[Accessed: 21-November-2024 ]}