AcousticPDEComponent
AcousticPDEComponent[vars,pars]
変数 vars,パラメータ pars で音響PDE項の成分を与える.
詳細




- AcousticPDEComponentは,偏微分演算子の一部として使われる微分演算子の和を返す.
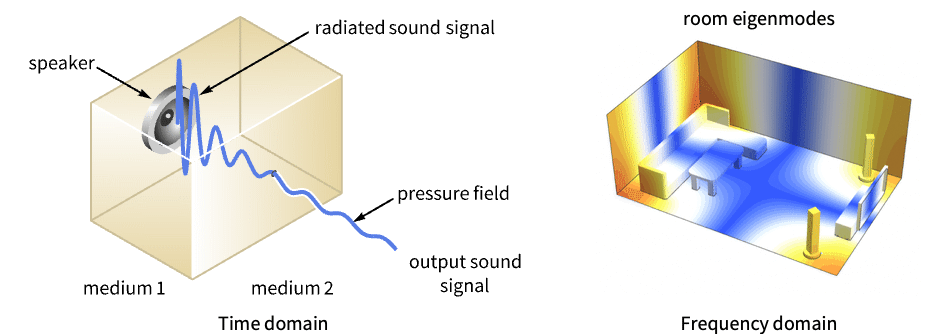
- AcousticPDEComponentは,時間領域と周波数領域の両方における等方性媒体中の音の伝播を拡散等のメカニズムによってモデル化する.
- AcousticPDEComponentは流体内の音響現象を従属変数圧力
 [
[![TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "Pa", pascals, "Pascals"}, QuantityTF]](Files/AcousticPDEComponent.ja/4.png) ],独立変数
],独立変数 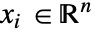 [
[![TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "m", meters, "Meters"}, QuantityTF]](Files/AcousticPDEComponent.ja/6.png) ],時間変数
],時間変数 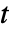 [
[![TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF] TemplateBox[{InterpretationBox[, 1], "s", seconds, "Seconds"}, QuantityTF]](Files/AcousticPDEComponent.ja/8.png) ] あるいは周波数変数
] あるいは周波数変数 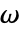 [
[![TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"rad", , "/", , "s"}, radians per second, {{(, "Radians", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/AcousticPDEComponent.ja/10.png) ]でモデル化する.
]でモデル化する. - 時間依存変数 vars は vars={p[t,x1,…,xn],t,{x1,…,xn}}である.
- 周波数依存変数 vars は vars={p[x1,…,xn],ω,{x1,…,xn}}である.
- 時間領域音響PDE AcousticPDEComponentは,時間変数
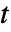 ,密度
,密度 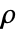 ,音速
,音速  ,音源
,音源 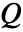 および
および 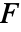 の波動方程式に基づいている.
の波動方程式に基づいている. - 周波数領域音響PDE AcousticPDEComponentは,角周波数
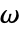 のヘルムホルツ(Helmholtz)方程式に基づいている.
のヘルムホルツ(Helmholtz)方程式に基づいている. - 音響モデル項の単位は[1/
![TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF]](Files/AcousticPDEComponent.ja/19.png) ]である.
]である. - 次のパラメータ pars を与えることができる.
-
パラメータ デフォルト シンボル "DipoleSource" {0,…}  ,二重極音源 [
,二重極音源 [![TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"N", , "/", , {"m", ^, 3}}, newtons per meter cubed, {{(, "Newtons", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/AcousticPDEComponent.ja/21.png) ]
]"MassDensity" 1  ,メディアの密度 [
,メディアの密度 [![TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"kg", , "/", , {"m", ^, 3}}, kilograms per meter cubed, {{(, "Kilograms", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]](Files/AcousticPDEComponent.ja/23.png) ]
]"Material" Automatic 
"MonopoleSource" 0  ,単極音源 [1/
,単極音源 [1/![TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {{"s", ^, 2}}, seconds squared, {"Seconds", ^, 2}}, QuantityTF]](Files/AcousticPDEComponent.ja/26.png) ]
]"RegionSymmetry" None 
"SoundSpeed" 1 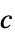 ,音速 [
,音速 [![TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF] TemplateBox[{InterpretationBox[, 1], {"m", , "/", , "s"}, meters per second, {{(, "Meters", )}, /, {(, "Seconds", )}}}, QuantityTF]](Files/AcousticPDEComponent.ja/29.png) ]
] - どのパラメータも,任意の
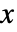 ,
,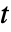 ,
,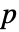 や他の従属変数に依存する可能性がある.例外として,
や他の従属変数に依存する可能性がある.例外として, は結果として非線形固有値問題になる.
は結果として非線形固有値問題になる. - AcousticPDEComponentには時間領域の音源および周波数領域の音源が使える.
-
単極音源, 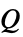
二重極音源, 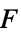
- 単極音源
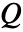 は音を等方的に放射する点音源をモデル化する.
は音を等方的に放射する点音源をモデル化する. - 二重極音源
 は音を非等方的に放射する2点音源をモデル化する.
は音を非等方的に放射する2点音源をモデル化する. - 独立変数(単位
 )の数は
)の数は 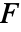 の長さを指定する.
の長さを指定する. - パラメータが指定されていなければ,デフォルトの時間領域音響PDEは以下のようになる.
- パラメータが指定されていなければ,デフォルトの周波数領域音響PDEは以下のようになる.
- パラメータの可能な選択肢には"RegionSymmetry"と"Axisymmetric"がある.
- "Axisymmetric"領域対称性は,以下のように角変数を除くことで円筒座標が縮小された切頭円筒座標系を表す.
-
次元 縮小 方程式 1D 
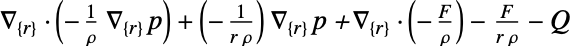
2D 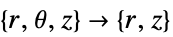
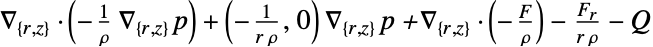
- AcousticPDEComponentが連想 piで…,keypi…,pivi,…]として指定されるパラメータ
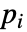 に依存するなら,パラメータ
に依存するなら,パラメータ  は
は  で置換される.
で置換される.
例題
すべて開くすべて閉じる例 (4)
スコープ (21)
時間領域 (7)
過渡音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
過渡音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
右側の音響インピーダンス境界とインピーダンス ![]() (
(![]() )で方程式を設定する:
)で方程式を設定する:
過渡音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端の音響粒子速度 v が ![]() である音響法線速度境界を持つ方程式を設定する:
である音響法線速度境界を持つ方程式を設定する:
過渡音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端に音圧境界と圧力源 ![]() (
(![]() )を持つ音響法線速度境界を持つ方程式を設定する:
)を持つ音響法線速度境界を持つ方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端に音響放射境界があり,圧力源が ![]() (
(![]() )で放射角度が
)で放射角度が ![]() (
(![]() )の方程式を設定する:
)の方程式を設定する:
過渡音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
周波数領域 (10)
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端に放射境界があり右端に音吸収境界がある方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端に放射境界,右端に音響インピーダンス境界,インピーダンス ![]() (
(![]() )の方程式を設定する:
)の方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端の音響法線速度境界,音粒子速度 ![]() (
(![]() ),右端の音吸収境界で方程式を設定する:
),右端の音吸収境界で方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端の音圧境界,圧力源 ![]() (
(![]() ),右端の音吸収境界で方程式を設定する:
),右端の音吸収境界で方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端の音放射境界,圧力源 ![]() (
(![]() ),放射角度
),放射角度 ![]() (
(![]() )で方程式を設定する:
)で方程式を設定する:
周波数領域音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
左端の音放射境界,圧力源 ![]() (
(![]() ),右端の音響ハード境界で方程式を設定する:
),右端の音響ハード境界で方程式を設定する:
アプリケーション (1)
以下の音響モデルは,振動ピストンがパイプの一端の内側に配置され,パイプの他端は無限領域に開いている,開管を表している.また,無条件領域をモデル化するためにインポーダンス境界条件が片端に置かれている.モデル化される管は,以下の図で示すように,フランジが付いた円管である:
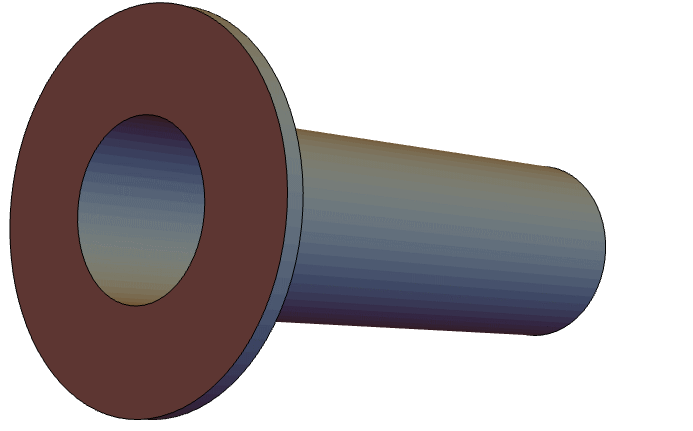
管の形状と境界条件は ![]() 軸について回転対称なので,軸対称モデルを使うことができる.音波の電波を表す支配方程式は軸対称ヘルムホルツ方程式である.
軸について回転対称なので,軸対称モデルを使うことができる.音波の電波を表す支配方程式は軸対称ヘルムホルツ方程式である.
軸対称の形状は,![]() 平面における管の断面を表す2Dの矩形で近似できる:
平面における管の断面を表す2Dの矩形で近似できる:
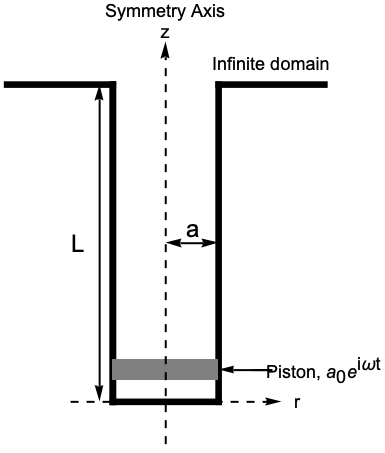
このモデルには2つの境界条件がある.一つは ![]() でピストンの加速
でピストンの加速 ![]() を表すNeumannValueである:
を表すNeumannValueである:
2番目の境界条件はインピーダンス ![]() のAcousticImpedanceValueである.インピーダンス
のAcousticImpedanceValueである.インピーダンス ![]() は以下の近似で与えられる.
は以下の近似で与えられる.![]() は波数である:
は波数である:
![]() で定義されたMaxCellMeasureおよび解像度12を使用して
で定義されたMaxCellMeasureおよび解像度12を使用して ![]() でPDEを解き,正確な結果を取得する:
でPDEを解き,正確な結果を取得する:
テキスト
Wolfram Research (2020), AcousticPDEComponent, Wolfram言語関数, https://reference.wolfram.com/language/ref/AcousticPDEComponent.html (2023年に更新).
CMS
Wolfram Language. 2020. "AcousticPDEComponent." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/AcousticPDEComponent.html.
APA
Wolfram Language. (2020). AcousticPDEComponent. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AcousticPDEComponent.html