AntisymmetricMatrixQ
Details and Options

- AntisymmetricMatrixQ is also known as skew-symmetric.
- A matrix m is antisymmetric if m-Transpose[m].
- AntisymmetricMatrixQ works for symbolic as well as numerical matrices.
- The following options can be given:
-
SameTest Automatic function to test equality of expressions Tolerance Automatic tolerance for approximate numbers - For exact and symbolic matrices, the option SameTest->f indicates that two entries mij and mkl are taken to be equal if f[mij,mkl] gives True.
- For approximate matrices, the option Tolerance->t can be used to indicate that all entries Abs[mij]≤t are taken to be zero.
- For matrix entries Abs[mij]>t, equality comparison is done except for the last
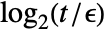 bits, where
bits, where 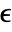 is $MachineEpsilon for MachinePrecision matrices and
is $MachineEpsilon for MachinePrecision matrices and 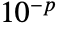 for matrices of Precision
for matrices of Precision 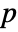 .
.
Examples
open all close allBasic Examples (2)
Scope (10)
Basic Uses (6)
Test if a real machine-precision matrix is antisymmetric:
A real antisymmetric matrix is also antihermitian:
Test if a complex matrix is antisymmetric:
A complex antisymmetric matrix has antisymmetric real and imaginary parts:
Test if an exact matrix is antisymmetric:
Make the matrix antisymmetric:
Use AntisymmetricMatrixQ with an arbitrary-precision matrix:
A random matrix is typically not antisymmetric:
Use AntisymmetricMatrixQ with a symbolic matrix:
The matrix becomes antisymmetric when ![]() and
and ![]() :
:
AntisymmetricMatrixQ works efficiently with large numerical matrices:
Special Matrices (4)
Use AntisymmetricMatrixQ with sparse matrices:
Use AntisymmetricMatrixQ with structured matrices:
Use with a QuantityArray structured matrix:
The identity matrix is not antisymmetric:
HilbertMatrix is not antisymmetric:
Options (2)
SameTest (1)
This matrix is antisymmetric for a positive real ![]() , but AntisymmetricMatrixQ gives False:
, but AntisymmetricMatrixQ gives False:
Use the option SameTest to get the correct answer:
Tolerance (1)
Generate a real-valued antisymmetric matrix with some random perturbation of order ![]() :
:
Adjust the option Tolerance to accept this matrix as antisymmetric:
The norm of the difference between the matrix and its transpose with opposite sign:
Applications (5)
Any matrix generated from an antisymmetric function ![]() is antisymmetric:
is antisymmetric:
The function is antisymmetric:
Using Table generates an antisymmetric matrix:
SymmetrizedArray can generate matrices (and general arrays) with symmetries:
Consider the family of rotation matrices corresponding to rotation by ![]() in the plane:
in the plane:
The logarithmic derivative ![]() is antisymmetric:
is antisymmetric:
This will be true of any 1-parameter family of rotations:
The cross product of two vectors can be expressed as a product of an antisymmetric matrix and a vector:
Find the function ![]() satisfying this time-dependent 3D equation:
satisfying this time-dependent 3D equation:
Represent the cross product by means of multiplication by the antisymmetric matrix ![]() :
:
Compute the exponential ![]() and use it to define a solution to the equation:
and use it to define a solution to the equation:
Verify that ![]() satisfies the differential equation and initial condition:
satisfies the differential equation and initial condition:
The matrix ![]() is orthogonal for all values of
is orthogonal for all values of ![]() :
:
Thus, the orbit of the solution is at a constant distance from the origin, in this case a circle:
Properties & Relations (15)
AntiymmetricMatrixQ[x] trivially returns False for any x that is not a matrix:
A matrix is antisymmetric if m-Transpose[m]:
An antisymmetric matrix must have zeros on the diagonal:
Use Diagonal to pick out the diagonal elements:
A real-valued antisymmetric matrix is antihermitian:
But a complex-valued antisymmetric matrix may not be:
Use Symmetrize with the symmetry Antisymmetric to compute the antisymmetric part of a matrix:
This equals the normalized difference between m and Transpose[m]:
Any matrix can be represented as the sum of its symmetric and antisymmetric parts:
Use SymmetricMatrixQ to test whether a matrix is symmetric:
If ![]() is an antisymmetric matrix with real entries, then
is an antisymmetric matrix with real entries, then ![]() is Hermitian:
is Hermitian:
MatrixExp[m] for real antisymmetric m is both orthogonal and unitary:
For complex antisymmetric m, the exponential is orthogonal but not, in general, unitary:
A real-valued antisymmetric matrix is always a normal matrix:
A complex-valued antisymmetric matrix need not be normal:
Real-valued antisymmetric matrices have pure imaginary eigenvalues:
Use Eigenvalues to find eigenvalues:
Note that a complex-valued antisymmetric matrix may have both real and complex eigenvalues:
Consider a real antisymmetric m of even dimensions:
CharacteristicPolynomial[m,x] contains only even powers of x:
For an odd-dimensioned m, the polynomial contains only odd powers:
Real-valued antisymmetric matrices have a complete set of eigenvectors:
As a consequence, they must be diagonalizable:
Use Eigenvectors to find the necessarily complex-valued eigenvectors:
Note that a complex-valued antisymmetric matrix need not have these properties:
Det[m] for antisymmetric m of odd dimensions is zero:
If m has even dimensions and its entries are real, its determinant is non-negative:
The inverse of an antisymmetric matrix is antisymmetric:
Possible Issues (1)
AntisymmetricMatrixQ uses the definition ![]() for both real- and complex-valued matrices:
for both real- and complex-valued matrices:
These complex matrices need not be normal or possess many properties of skew-adjoint (real antisymmetric) matrices:
AntihermitianMatrixQ tests the condition ![]() for skew-adjoint matrices:
for skew-adjoint matrices:
Alternatively, test if the entries are real to restrict to real symmetric matrices:
Related Guides
History
Text
Wolfram Research (2014), AntisymmetricMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/AntisymmetricMatrixQ.html.
CMS
Wolfram Language. 2014. "AntisymmetricMatrixQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AntisymmetricMatrixQ.html.
APA
Wolfram Language. (2014). AntisymmetricMatrixQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AntisymmetricMatrixQ.html
BibTeX
@misc{reference.wolfram_2025_antisymmetricmatrixq, author="Wolfram Research", title="{AntisymmetricMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/AntisymmetricMatrixQ.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_antisymmetricmatrixq, organization={Wolfram Research}, title={AntisymmetricMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/AntisymmetricMatrixQ.html}, note=[Accessed: 25-January-2026]}

