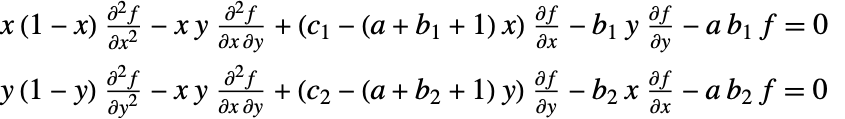AppellF2

AppellF2[a,b1,b2,c1,c2,x,y]

二変数のアッペル(Appell)超幾何関数 である．

詳細

  • AppellF2は，超幾何級数を一般化して多項式係数を持つHorn偏微分方程式系を解くAppell関数族の一員である．
  • 記号操作・数値操作の両方に適した数学関数である．
  • は，領域TemplateBox[{x}, Abs]+TemplateBox[{y}, Abs]<1内で収束する超幾何級数 を介して主定義を得る．引数の実数値についてのAppellF2級数の収束領域は以下の通りである．
  • 引数の実数値についてのアッペルF2級数の収束領域は以下の通りである．
  • 一般に，は の形のHorn偏微分方程式系を満足する． »
  • は または のときに簡約される．
  • 特別な引数の場合，AppellF2は自動的に厳密値を計算する．
  • AppellF2は任意の数値精度で評価できる．

例題

すべて開くすべて閉じる

例  (7)

数値的に評価する：

総和の定義：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

AppellF2関数族をプロットする：

原点における級数展開：

TraditionalFormによる表示：

スコープ  (17)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素数入力：

AppellF2を高精度で効率的に評価する：

Aroundを使って平均的な場合の統計区間を計算する：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のAppellF2関数を計算することもできる：

特定の値  (3)

固定点における値：

Hypergeometric2F1関数に簡約する：

ゼロにおける値：

可視化  (3)

AppellF2関数をさまざまなパラメータについてプロットする：

AppellF2をその第2パラメータ の関数としてプロットする：

の実部をプロットする：

の虚部をプロットする：

微分  (4)

x についての一次導関数：

y についての一次導関数：

y についてのより高次の導関数：

a=b1=b2=2，c1=c2=5，x=1/5のときの y についてのより高次の導関数をプロットする：

y についての 次導関数の式：

級数展開  (1)

Seriesを使ってテイラー(Taylor)展開を求める：

の周りの最初の3つの近似のプロット：

アプリケーション  (1)

アッペル関数 は多項式係数を持つ以下の偏微分方程式系を解く：

が解であることを確かめる：

おもしろい例題  (1)

多くの初等関数および特殊関数はAppellF2の特殊ケースである：

Wolfram Research (2023), AppellF2, Wolfram言語関数， https://reference.wolfram.com/language/ref/AppellF2.html.

テキスト

Wolfram Research (2023), AppellF2, Wolfram言語関数， https://reference.wolfram.com/language/ref/AppellF2.html.

CMS

Wolfram Language. 2023. "AppellF2." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AppellF2.html.

APA

Wolfram Language. (2023). AppellF2. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AppellF2.html

BibTeX

@misc{reference.wolfram_2024_appellf2, author="Wolfram Research", title="{AppellF2}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/AppellF2.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_appellf2, organization={Wolfram Research}, title={AppellF2}, year={2023}, url={https://reference.wolfram.com/language/ref/AppellF2.html}, note=[Accessed: 05-November-2024 ]}