AppellF4

AppellF4[a,b,c1,c2,x,y]

is the Appell hypergeometric function of two variables .

Details

  • AppellF4 belongs to the family of Appell functions that generalize the hypergeometric series and solves the system of Horn PDEs with polynomial coefficients.
  • Mathematical function, suitable for both symbolic and numerical manipulation.
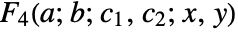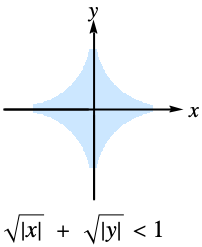
  • has a primary definition through the hypergeometric series 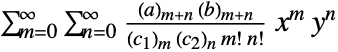, which is convergent inside the region sqrt(TemplateBox[{x}, Abs])+sqrt(TemplateBox[{y}, Abs])<1.
  • The region of convergence of the Appell F4 series for real values of its arguments is the following:
  • In general, 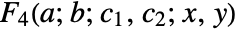satisfies the following Horn PDE system »: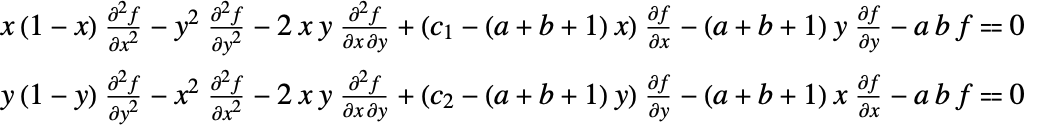
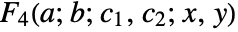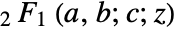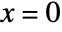  • reduces to when or .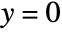
  • For certain special arguments, AppellF4 automatically evaluates to exact values.
  • AppellF4 can be evaluated to arbitrary numerical precision.

Examples

open allclose all

Basic Examples  (7)

Evaluate numerically:

The defining sum:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Plot a family of AppellF4 functions:

Series expansion at the origin:

TraditionalForm formatting:

Scope  (17)

Numerical Evaluation  (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate AppellF4 efficiently at high precision:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix AppellF4 function using MatrixFunction:

Specific Values  (3)

Values at fixed points:

Simplify to Hypergeometric2F1 functions:

Value at zero:

Visualization  (3)

Plot the AppellF4 function for various parameters:

Plot AppellF4 as a function of its second parameter :

Plot the real part of :

Plot the imaginary part of :

Differentiation  (4)

First derivative with respect to x:

First derivative with respect to y:

Higher derivatives with respect to y:

Plot the higher derivatives with respect to y when a=1/2, b=3/2, c1=1/3, c2=4 and x=1/5:

Formula for the ^(th) derivative with respect to y:

Series Expansions  (1)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Applications  (1)

The Appell function solves the following system of PDEs with polynomial coefficients:

Check that is a solution:

Neat Examples  (1)

Many elementary and special functions are special cases of AppellF4:

Wolfram Research (2023), AppellF4, Wolfram Language function, https://reference.wolfram.com/language/ref/AppellF4.html.

Text

Wolfram Research (2023), AppellF4, Wolfram Language function, https://reference.wolfram.com/language/ref/AppellF4.html.

CMS

Wolfram Language. 2023. "AppellF4." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/AppellF4.html.

APA

Wolfram Language. (2023). AppellF4. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AppellF4.html

BibTeX

@misc{reference.wolfram_2024_appellf4, author="Wolfram Research", title="{AppellF4}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/AppellF4.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_appellf4, organization={Wolfram Research}, title={AppellF4}, year={2023}, url={https://reference.wolfram.com/language/ref/AppellF4.html}, note=[Accessed: 21-December-2024 ]}