ArcCosh

ArcCosh[z]

複素数 の逆双曲線余弦を与える．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．
  • 特別な引数の場合，ArcCoshは自動的に厳密値を計算する．
  • ArcCoshは任意の数値精度で評価できる．
  • ArcCoshは自動的にリストに関数の並列的な適用を行う．
  • ArcCosh[z]は，複素 平面上，〜の範囲で不連続な分枝切断線を持つ．
  • ArcCoshはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる． »

予備知識

  • ArcCoshは，逆双曲線余弦関数である．ArcCosh[x]は，実数 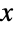について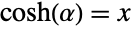， となるような 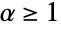の双曲線角度を表す．
  • ArcCoshは自動的にリストに縫い込まれる．特別な引数の場合，ArcCoshは自動的に厳密値を計算する．厳密な数式が引数として与えられると，ArcCoshは任意の数値精度に評価できることがある．ArcCoshを含む記号式の操作に便利なその他の演算には，FunctionExpand，TrigToExp，TrigExpand，Simplify，FullSimplifyがある．
  • ArcCoshは，複素引数 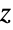について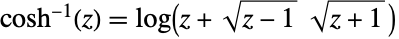，によって定義される．ArcCosh[z]は複素 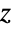平面上で不連続な分枝切断線を持つ．
  • 関連する数学関数には，Cosh，ArcSinh，ArcCosがある．

例題

すべて開くすべて閉じる

例  (5)

数値的に評価する：

実数の部分集合上でプロットする：

複素数の部分集合上でプロットする：

Infinityにおける漸近展開：

特異点における漸近展開：

スコープ  (41)

数値評価  (6)

数値的に評価する：

高精度で評価する：

出力精度は入力精度に従う：

複素引数について評価する：

ArcCoshを高精度で効率よく評価する：

IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する：

Aroundを使って平均的な場合の統計区間を計算することもできる：

配列の要素ごとの値を計算する：

MatrixFunctionを使って行列のArcCosh関数を計算することもできる：

特定の値  (4)

固定点におけるArcCoshの値：

無限大における値：

ArcCoshの零点：

方程式 を満足する の値を求める：

値を代入する：

結果を可視化する：

可視化  (3)

ArcCosh関数をプロットする：

の実部をプロットする：

の虚部をプロットする：

での極プロット：

関数の特性  (10)

ArcCoshは，1以上のすべての実数値について定義される：

複素領域は平面全体である：

ArcCoshは0以上のすべての実数値に達する：

複素領域からの引数についての関数領域：

ArcCoshは解析関数ではない：

有理型でもない：

ArcCoshは実数領域で増加する：

ArcCoshは単射である：

ArcCoshは全射ではない：

ArcCoshは実数領域上で非負である：

(-∞,1]に特異点と不連続点の両方を持つ：

ArcCoshは実数領域上で凹である：

TraditionalFormによる表示：

微分  (3)

一次導関数：

高次導関数：

次導関数の式：

積分  (3)

ArcCoshの不定積分：

実領域外の区間上のArcCoshの定積分は虚部である：

その他の積分例：

級数展開  (4)

Seriesを使ってテイラー(Taylor)展開を求める：

付近でArcCoshについての最初の3つの近似をプロットする：

付近でのArcCoshの級数展開における一般項：

分岐点および分枝切断線における級数展開を求める：

ArcCoshはベキ級数に適用できる：

関数の恒等式と簡約  (3)

ArcCoshを含む式を簡約する：

TrigToExpを使って，対数と平方根を介して表現する：

変換し直す：

実変数の および を仮定して展開する：

関数表現  (5)

ArcSechを使って表現する：

ヤコビ関数の逆関数を介して表現する：

Hypergeometric2F1を使って表現する：

ArcCoshはMeijerGによって表すことができる：

ArcCoshはDifferentialRootとして表すことができる：

アプリケーション  (4)

本体のエネルギーを静止エネルギーの2倍に押し上げる速さを求める：

必要な光速に対する割合：

ミズーリ州セントルイスにあるゲートウェイアーチの反転した懸垂形アーチの底辺の幅をフィートで：

ArcCoshの実部と虚部をプロットする：

微分方程式を解く：

特性と関係  (5)

逆関数を使った構成には，PowerExpandによって恒等式まで簡約する必要があるかもしれない：

代りに，追加的な仮定を使うことができる：

次は，ArcCosh関数の分枝切断線を示している：

逆三角方程式を解く：

ゼロについて解く：

ArcCoshが満足する微分方程式を解く：

これがArcCoshを満足することを証明する：

考えられる問題  (2)

一般に である：

分枝切断線上では，機械精度の入力が数値的に正しくない答を与えることがある：

おもしろい例題  (1)

Wolfram Research (1988), ArcCosh, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcCosh.html （2021年に更新）.

テキスト

Wolfram Research (1988), ArcCosh, Wolfram言語関数， https://reference.wolfram.com/language/ref/ArcCosh.html （2021年に更新）.

CMS

Wolfram Language. 1988. "ArcCosh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/ArcCosh.html.

APA

Wolfram Language. (1988). ArcCosh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcCosh.html

BibTeX

@misc{reference.wolfram_2024_arccosh, author="Wolfram Research", title="{ArcCosh}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/ArcCosh.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arccosh, organization={Wolfram Research}, title={ArcCosh}, year={2021}, url={https://reference.wolfram.com/language/ref/ArcCosh.html}, note=[Accessed: 21-November-2024 ]}