ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]
creates a single flattened matrix from a matrix of matrices mi j.
ArrayFlatten[a,r]
flattens out r pairs of levels in the array a.


ArrayFlatten
ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]
creates a single flattened matrix from a matrix of matrices mi j.
ArrayFlatten[a,r]
flattens out r pairs of levels in the array a.
Details

- ArrayFlatten requires that the blocks it flattens have dimensions that fit together.
- ArrayFlatten can be used to form block matrices from arrays of blocks.
- For a matrix of matrices, ArrayFlatten[a] yields a matrix whose elements are in the same order as in MatrixForm[a].
- ArrayFlatten[a] is normally equivalent to Flatten[a,{{1,3},{2,4}}]. »
- ArrayFlatten[a,r] is normally equivalent to Flatten[a,{{1,r+1},{2,r+2},…,{r,2r}}].
- For a tensor with rank 2r, ArrayFlatten[a,r] gives a tensor with rank r.
- In ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}], all the matrices mi j in the same row must have the same first dimension, and matrices mi j in the same column must have the same second dimension.
- In general, in ArrayFlatten[a,r], all the k
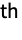 dimensions of a[[i1,i2,…,
dimensions of a[[i1,i2,…,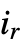 ]] must be equal for each possible value of ik .
]] must be equal for each possible value of ik . - Elements at level r whose array depth is less than r are treated as scalars, and are replicated to fill out a rank-r array of the appropriate dimensions.
- ArrayFlatten works with SparseArray objects. »
Examples
open all close allBasic Examples (2)
Scope (4)
Flatten a rank-4 array to rank 2:
Flatten only the first four levels of a rank-6 array:
Flatten a rank 6 array to rank 3:
ArrayFlatten works with SparseArray objects:
Make a sparse matrix from a block matrix of SparseArray objects:
Applications (5)
Put together many copies of a "tile":
Iterate a 2D substitution system:
Iterate a 3D substitution system:
Form an involutory matrix ![]() , such that
, such that ![]() :
:
Check that the resulting matrix is involutory:
Form a block matrix semidiscretization of the wave equation ![]() with n spatial points:
with n spatial points:
Differentiation matrix for second-order approximation of ![]() with periodic boundary conditions:
with periodic boundary conditions:
Form block matrix a for system ![]() where
where ![]() :
:
Set up an initial condition vector for ![]() :
:
Approximate the solution at ![]() using the backward Euler method with time step k:
using the backward Euler method with time step k:
Properties & Relations (3)
MatrixForm displays matrices of matrices in the same order as ArrayFlatten:
ArrayFlatten is a special case of Flatten:
KroneckerProduct is defined as ArrayFlatten of an Outer product:
See Also
Flatten Join Band ArrayQ ArrayDepth ArrayPad ImageApply SubstitutionSystem ArrayReduce
Function Repository: BlockDiagonalMatrix
Tech Notes
History
Text
Wolfram Research (2007), ArrayFlatten, Wolfram Language function, https://reference.wolfram.com/language/ref/ArrayFlatten.html.
CMS
Wolfram Language. 2007. "ArrayFlatten." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayFlatten.html.
APA
Wolfram Language. (2007). ArrayFlatten. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayFlatten.html
BibTeX
@misc{reference.wolfram_2025_arrayflatten, author="Wolfram Research", title="{ArrayFlatten}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayFlatten.html}", note=[Accessed: 02-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_arrayflatten, organization={Wolfram Research}, title={ArrayFlatten}, year={2007}, url={https://reference.wolfram.com/language/ref/ArrayFlatten.html}, note=[Accessed: 02-December-2025]}