ArrayFlatten
ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]
行列 mi jの行列から単一の平坦化された行列を作成する.
ArrayFlatten[a,r]
配列 a 中の r 組のペアになったレベルを平坦化する.
詳細

- ArrayFlattenが平坦化するブロックは整合性がなければならない.
- ArrayFlattenは,ブロックの配列からブロック行列を形成するのに使うことができる.
- 行列の行列の場合,ArrayFlatten[a]は要素の並び順がMatrixForm[a]と同じ行列を返す.
- ArrayFlatten[a]は一般にFlatten[a,{{1,3},{2,4}}]と等しい. »
- ArrayFlatten[a,r]は一般にFlatten[a,{{1,r+1},{2,r+2},…,{r,2r}}]と等しい.
- 階数2r のテンソルの場合,ArrayFlatten[a,r]は階数 r のテンソルを返す.
- ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]では,同じ行内のすべての行列 mi jが同一の最初の次元でなければならず,同じ列内の行列 mi jは同一の2番目の次元でなければならない.
- 一般に,ArrayFlatten[a,r]において,a[[i1,i2,…,
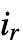 ]]のすべての k
]]のすべての k 番目の次元は ik のそれぞれの可能な値について等しくなければならない.
番目の次元は ik のそれぞれの可能な値について等しくなければならない. - 配列の深さが r より小さいレベル r の要素はスカラーとして扱われ,適切な次元の階数 r の配列を埋めるのに繰り返される.
- ArrayFlattenはSparseArrayオブジェクトに使うことができる. »
例題
すべて開くすべて閉じるスコープ (4)
ArrayFlattenはSparseArrayオブジェクトに使うことができる:
SparseArrayオブジェクトのブロック行列から疎行列を作る:
アプリケーション (5)
特性と関係 (3)
MatrixFormは行列の行列をArrayFlattenと同じ順序で表示する:
ArrayFlattenはFlattenの特殊ケースである:
KroneckerProductはOuter積のArrayFlattenとして定義される:
テキスト
Wolfram Research (2007), ArrayFlatten, Wolfram言語関数, https://reference.wolfram.com/language/ref/ArrayFlatten.html.
CMS
Wolfram Language. 2007. "ArrayFlatten." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayFlatten.html.
APA
Wolfram Language. (2007). ArrayFlatten. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArrayFlatten.html