ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]
由矩阵 mi j 组成的矩阵,创建一个单一的展平矩阵.
ArrayFlatten[a,r]
在数组 a 中,展平 r 对层次.


ArrayFlatten
ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}]
由矩阵 mi j 组成的矩阵,创建一个单一的展平矩阵.
ArrayFlatten[a,r]
在数组 a 中,展平 r 对层次.
更多信息

- ArrayFlatten 要求它展平的块具有相适应的维数.
- ArrayFlatten 可用于由数组块形成块矩阵.
- 针对矩阵组的一个矩阵而言,ArrayFlatten[a] 所生成矩阵的元素次序和 MatrixForm[a] 相同.
- ArrayFlatten[a] 通常等价于 Flatten[a,{{1,3},{2,4}}]. »
- ArrayFlatten[a,r] 通常等价于 Flatten[a,{{1,r+1},{2,r+2},…,{r,2r}}].
- 对于一个秩为 2r 的张量而言,ArrayFlatten[a,r] 给出一个秩为 r 的张量.
- 在 ArrayFlatten[{{m11,m12,…},{m21,m22,…},…}] 中,同一行的所有矩阵 mi j 必须具有相同的第一维,同一列中的矩阵 mi j 必须具有相同的第二维.
- 通常在 ArrayFlatten[a,r] 中,对于 ik 的每一可能值,所有 a[[i1,i2,…,
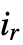 ]] 的第 k
]] 的第 k 维数必须相等.
维数必须相等. - 数组深度小于 r 的第 r 层次元素的作为标量处理,并且被复制用于填入一个相应维数的秩为 r 的数组.
- ArrayFlatten 对 SparseArray 对象起作用. »
范例
打开所有单元 关闭所有单元范围 (4)
ArrayFlatten 对 SparseArray 对象起作用:
从一个 SparseArray 对象的块矩阵生成一个稀疏矩阵:
应用 (5)
属性和关系 (3)
MatrixForm 按照和 ArrayFlatten 相同的次序显示矩阵组的矩阵:
ArrayFlatten 是 Flatten 的一个特例:
KroneckerProduct 定义为一个 Outer 积的 ArrayFlatten:
参见
Flatten Join Band ArrayQ ArrayDepth ArrayPad ImageApply SubstitutionSystem ArrayReduce
Function Repository: BlockDiagonalMatrix
文本
Wolfram Research (2007),ArrayFlatten,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ArrayFlatten.html.
CMS
Wolfram 语言. 2007. "ArrayFlatten." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ArrayFlatten.html.
APA
Wolfram 语言. (2007). ArrayFlatten. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ArrayFlatten.html 年
BibTeX
@misc{reference.wolfram_2025_arrayflatten, author="Wolfram Research", title="{ArrayFlatten}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/ArrayFlatten.html}", note=[Accessed: 20-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_arrayflatten, organization={Wolfram Research}, title={ArrayFlatten}, year={2007}, url={https://reference.wolfram.com/language/ref/ArrayFlatten.html}, note=[Accessed: 20-February-2026]}