AsymptoticGreater[f,g,xx*]
给出当 xx* 时 ![]() 或
或 ![]() 的条件.
的条件.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
给出当 ![]() 时
时 ![]() 或
或 ![]() 的条件.
的条件.


AsymptoticGreater
AsymptoticGreater[f,g,xx*]
给出当 xx* 时 ![]() 或
或 ![]() 的条件.
的条件.
AsymptoticGreater[f,g,{x1,…,xn}{![]() ,…,
,…,![]() }]
}]
给出当 ![]() 时
时 ![]() 或
或 ![]() 的条件.
的条件.
更多信息和选项


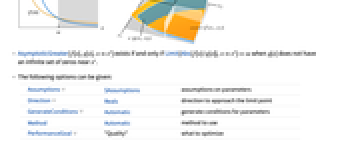

- 渐近大于也被表示为 f 是 g 的小写的 omega,f 的大小大于 g,f 比 g 增长得快,f 强于 g. 经常从上下文中估计点 x*.
- 渐近大于是一种排序关系,意味着对于所有常数
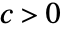 ,当 x 靠近 x* 时,
,当 x 靠近 x* 时,![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.zh/9.png) .
. - 典型的用途包括表示函数和序列在一些点附近的简单严格下界. 它经常用于方程的解,并给出计算复杂度的简单严格下界.
- 对于有限极限点 x* 和 {
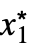 ,…,
,…,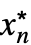 }:
}: -
AsymptoticGreater[f[x],g[x],xx*] 对于所有的 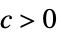 ,存在
,存在 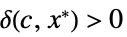 使得
使得 ![0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*) 0<TemplateBox[{{x, -, {x, ^, *}}}, Abs]<delta(c,x^*)](Files/AsymptoticGreater.zh/14.png) 意味着
意味着 ![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.zh/15.png) 成立
成立AsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{ 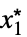 ,…,
,…,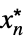 }]
}]对于所有的 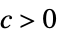 ,存在
,存在 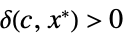 使得
使得 ![0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*) 0<TemplateBox[{{{, {{{x, _, 1}, -, {x, _, {(, 1, )}, ^, *}}, ,, ..., ,, {{x, _, n}, -, {x, _, {(, n, )}, ^, *}}}, }}}, Norm]<delta(epsilon,x^*)](Files/AsymptoticGreater.zh/20.png) 意味着
意味着 ![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.zh/21.png) 成立
成立 - 对于无限极限点:
-
AsymptoticGreater[f[x],g[x],x∞] 对于所有的 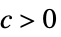 ,存在
,存在 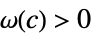 使得
使得 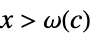 意味着
意味着 ![TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs] TemplateBox[{{f, (, x, )}}, Abs]>=c TemplateBox[{{g, (, x, )}}, Abs]](Files/AsymptoticGreater.zh/26.png) 成立
成立AsymptoticGreater[f[x1,…,xn],g[x1,…,xn],{x1,…,xn}{∞,…,∞}] 对于所有的 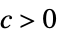 ,存在
,存在 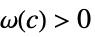 使得
使得 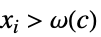 意味着
意味着 ![TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs] TemplateBox[{{f, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]>=c TemplateBox[{{g, (, {{x, _, 1}, ,, ..., ,, {x, _, n}}, )}}, Abs]](Files/AsymptoticGreater.zh/30.png) 成立
成立 - 在 x* 附近 g[x] 的值不为无限个零时,当且仅当 Limit[Abs[f[x]/g[x]],xx*]∞ 成立时, AsymptoticGreater[f[x],g[x],xx*] 才存在.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数的设定 Direction Reals 趋近极限点的方向 GenerateConditions Automatic 对参数生成条件 Method Automatic 所使用的方法 PerformanceGoal "Quality" 优化目标 - Direction 的可能设置包括:
-
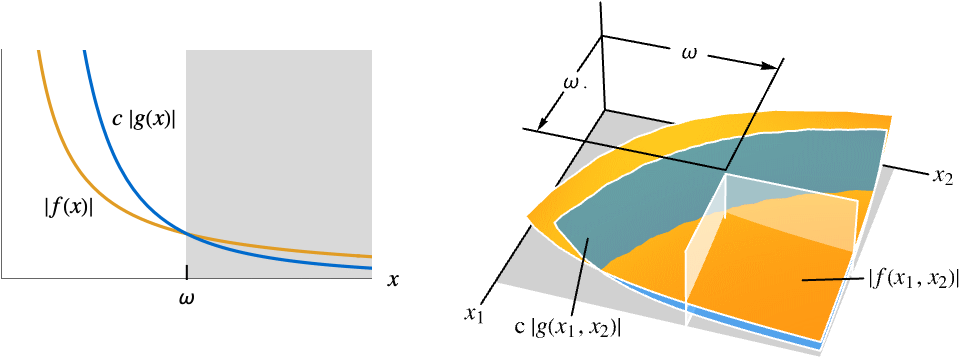
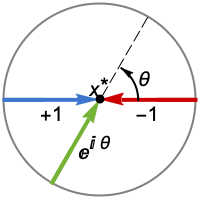
Reals or "TwoSided" 从两个实方向 "FromAbove" or -1 从上面或较大的值 "FromBelow" or +1 从下面或较小的值 Complexes 从所有复方向 Exp[ θ] 从方向 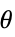
{dir1,…,dirn} 对变量 xi 分别使用方向 diri - 在 x* 处的 DirectionExp[ θ] 表示接近极限点 x* 的曲线的方向切线.
- GenerateConditions 的可能设置包括:
-
Automatic 只给出非通用条件 True 所有条件 False 不给出条件 None 如果需要条件则不经计算直接返回 - PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 当设置为 "Quality" 时,AsymptoticGreater 通常可以解出更多的问题或者产生更简单的结果,但是可能会耗费更多的时间和内存.
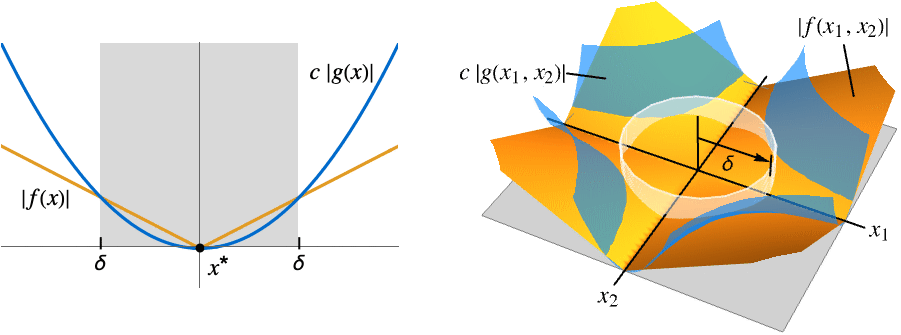
范例
打开所有单元 关闭所有单元范围 (9)
选项 (10)
Assumptions (1)
用 Assumptions 为参数指定条件:
Direction (5)
GenerateConditions (3)
当 GenerateConditions->True 时,非通用条件也要报告:
PerformanceGoal (1)
用 PerformanceGoal 来避免潜在的巨量计算:
应用 (18)
基本应用 (4)
绝对和相对误差 (2)
渐近近似 (6)
设 ![]() 为一个函数,
为一个函数,![]() 是
是 ![]() 在
在 ![]() 附近的近似. 如果在
附近的近似. 如果在 ![]() 处
处 ![]() ,则近似是渐近的. 换句话说,余数或误差
,则近似是渐近的. 换句话说,余数或误差 ![]() 渐近小于近似值. 证明
渐近小于近似值. 证明 ![]() 是
是 ![]() 在
在 ![]() 处的渐近近似值:
处的渐近近似值:
Series 可以生成基本函数和特殊函数的渐近近似. 例如,生成 ![]() 在
在 ![]() 处的 10 次 (degree-10) 近似:
处的 10 次 (degree-10) 近似:
给出 Cot[x] 在 0 处的渐近级数:
证明 Gamma[x] 的级数在 -1 处是渐近级数:
当要近似的函数在近似点的每个邻域中无限多次逼近于零时,渐近近似可能会有微妙的变化. 作为一个例子,我们来考虑 ![]() 在
在 ![]() 附近的渐近展开式:
附近的渐近展开式:
近似不是渐近的,因为在贝塞尔函数的每个零点上近似值都不是零:
另一方面,我们来考虑永远非零的 Hankel 函数 ![]() 的近似:
的近似:
由于 ![]() ,作为两个这种近似的和,它的近似可以理解为几乎是渐近的:
,作为两个这种近似的和,它的近似可以理解为几乎是渐近的:
用 AsymptoticIntegrate 来生成定积分的渐近近似. 例如,求 ![]() 在
在 ![]() 时的渐近近似,并与精确值进行比较:
时的渐近近似,并与精确值进行比较:
用 AsymptoticIntegrate 来生成不定积分的渐近近似,尽管要考虑积分常数. 求 ![]() 在
在 ![]() 时的近似:
时的近似:
用 AsymptoticDSolveValue 生成微分方程的渐近近似:
与通过 NDSolveValue 获得的数值解进行比较:
渐近尺度 (2)
计算复杂度 (4)
简单的排序算法(冒泡排序,插入排序)需要大约 a n2 个步骤对 n 个对象进行排序,而最优通用算法(堆排序,合并排序)大约需要 b n Log[n] 个步骤来进行排序. 证明对足够大的对象集合进行排序时,最优算法总是花费更少的时间:
某些特殊的算法(计数排序,基数排序),在有关可能的输入的信息提前存在的情况下,可在 c n 时间内完成. 当可以使用这些算法时,它们甚至比最优算法更快:
在冒泡排序中,对相邻的项进行比较,如果顺序不对即进行交换. 经过 n-1 次比较后,最大的元素在最后. 然后在剩余的 n-1 个元素上重复该过程,直到开头处只剩下两个元素. 如果比较和交换需要 c 个步骤,则排序需要的总步骤如下所示:
在合并排序中,元素列表被分成两部分,分别对每部分进行排序,然后合并两个部分. 因此,进行排序的总时间 T[n] 将是用于计算中值的某个固定时间 b 加上对每一半元素进行排序的时间 2T[n/2],再加上用于将两部分元素合并在一起的时间,即元素个数的倍数 a n:
旅行推销员问题 (TSP) 需要找到连接 ![]() 个城市的最短路线. 一个朴素的算法是尝试所有
个城市的最短路线. 一个朴素的算法是尝试所有 ![]() 个路线. Held–Karp 算法将其减少到大约
个路线. Held–Karp 算法将其减少到大约 ![]() 个步骤. 证明
个步骤. 证明 ![]() ,因此 Held–Karp 算法更快:
,因此 Held–Karp 算法更快:
这两种算法都表明,TSP 的计算复杂度类不比 EXPTIME 难,EXPTIME 问题是可以在时间 ![]() 内解决的问题. 对于 Held–Karp 算法,使用
内解决的问题. 对于 Held–Karp 算法,使用 ![]() 就可以了,其中
就可以了,其中 ![]() :
:
可以在 ![]() 时间内找到近似解,所以近似 TSP 属于复杂度类 P 问题,是在多项式时间内可以解决的问题. 任何多项式算法都比指数型算法快,或
时间内找到近似解,所以近似 TSP 属于复杂度类 P 问题,是在多项式时间内可以解决的问题. 任何多项式算法都比指数型算法快,或 ![]() :
:
属性和关系 (10)
AsymptoticGreater 是不自反的,即 ![]() :
:
当且仅当 Limit[Abs[f[x]/g[x]],xx0]∞ 时,AsymptoticGreater[f[x],g[x],xx0] 的结果为:
相关指南
-
▪
- 渐近
文本
Wolfram Research (2018),AsymptoticGreater,Wolfram 语言函数,https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
CMS
Wolfram 语言. 2018. "AsymptoticGreater." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/AsymptoticGreater.html.
APA
Wolfram 语言. (2018). AsymptoticGreater. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/AsymptoticGreater.html 年
BibTeX
@misc{reference.wolfram_2025_asymptoticgreater, author="Wolfram Research", title="{AsymptoticGreater}", year="2018", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticGreater.html}", note=[Accessed: 05-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_asymptoticgreater, organization={Wolfram Research}, title={AsymptoticGreater}, year={2018}, url={https://reference.wolfram.com/language/ref/AsymptoticGreater.html}, note=[Accessed: 05-February-2026]}