BSplineBasis

BSplineBasis[d,x]

gives the zeroth uniform B-spline basis function of degree d at x.

BSplineBasis[d,n,x]

gives the n^(th) uniform B-spline basis function of degree d.

BSplineBasis[{d,{u1,u2,…}},n,x]

gives the n^(th) non-uniform B-spline basis function of degree d with knots at positions ui.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • BSplineBasis[d,x] is equivalent to BSplineBasis[d,0,x].
  • BSplineBasis[d,n,x] gives B-spline basis functions that have nonzero values only within the x interval between 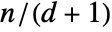and .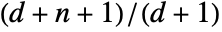
  • BSplineBasis[{d,{u1,u2,…,um}},n,x] gives B-spline basis functions that have nonzero values only within the x interval between u1 and um.
  • The knot positions ui must form a non-decreasing sequence.
  • Possible values of n range from 0 to m-d-2.
  • PiecewiseExpand can be used to expand symbolic BSplineBasis functions into explicit piecewise polynomials.

Examples

open allclose all

Basic Examples  (4)

Evaluate a uniform cubic B-spline basis numerically:

Plot it:

Evaluate the second cubic B-spline basis with given knots:

Plot all the cubic basis functions with given knots:

Symbolic derivative of B-spline basis:

Plot of the derivatives:

Scope  (1)

TraditionalForm formatting:

Properties & Relations  (3)

The nonzero part of a B-spline basis function is given by the range of knots:

The sum of all B-spline bases at points within the support is always one:

At most, d+1 basis functions contribute to the sum where d is the degree:

BSplineBasis can be used to build up BSplineCurve:

Wolfram Research (2008), BSplineBasis, Wolfram Language function, https://reference.wolfram.com/language/ref/BSplineBasis.html.

Text

Wolfram Research (2008), BSplineBasis, Wolfram Language function, https://reference.wolfram.com/language/ref/BSplineBasis.html.

CMS

Wolfram Language. 2008. "BSplineBasis." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BSplineBasis.html.

APA

Wolfram Language. (2008). BSplineBasis. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BSplineBasis.html

BibTeX

@misc{reference.wolfram_2024_bsplinebasis, author="Wolfram Research", title="{BSplineBasis}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BSplineBasis.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bsplinebasis, organization={Wolfram Research}, title={BSplineBasis}, year={2008}, url={https://reference.wolfram.com/language/ref/BSplineBasis.html}, note=[Accessed: 14-November-2024 ]}