WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

BesselJZero
✖
BesselJZero

✖

represents the k^(th) zero of the Bessel function .

✖
BesselJZero[n,k,x0]

represents the k^(th) zero greater than x0.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • N[BesselJZero[n,k]] gives a numerical approximation so long as the specified zero exists.
  • BesselJZero[n,k] represents the k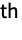^(th) zero greater than 0.
  • BesselJZero can be evaluated to arbitrary numerical precision.
  • BesselJZero automatically threads over lists. »

Examples

open allclose all

Basic Examples  (5)Summary of the most common use cases

Evaluate numerically:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-mng3w
Out[1]=1

Evaluate symbolically:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-clelng
Out[1]=1

Display zeros of the BesselJ function over a subset of the reals:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-b44iq5
Out[1]=1

Series expansion at the origin:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-qhqqh
Out[1]=1

TraditionalForm formatting:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-fm3bjb

Scope  (18)Survey of the scope of standard use cases

Numerical Evaluation  (7)

Evaluate numerically:

In[3]:=3
✖
https://wolfram.com/xid/0mlgadgcsomw-l274ju
Out[3]=3

Find the first zero of greater than 40:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-gvjp4u
Out[1]=1

Evaluate to high precision:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-b0wt9
Out[1]=1

Evaluate efficiently at high precision:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-di5gcr
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlgadgcsomw-bq2c6r
Out[2]=2

Evaluate at a non-integer second argument:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-fegr0a
Out[1]=1

For BesselJZero[ν,k-α/π], the result is a zero of :

In[2]:=2
✖
https://wolfram.com/xid/0mlgadgcsomw-jyn2na
Out[2]=2

Compute average-case statistical intervals using Around:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-cw18bq
Out[1]=1

Compute the elementwise values of an array using automatic threading:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-thgd2
Out[1]=1

Or compute the matrix BesselJZero function using MatrixFunction:

In[2]:=2
✖
https://wolfram.com/xid/0mlgadgcsomw-o5jpo
Out[2]=2

Specific Values  (3)

Limiting value at infinity:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-ciezym
Out[1]=1

The first three zeros:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-e3n9bq
Out[1]=1

Find the first zero of BesselJ[1,x] using Solve:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-f2hrld
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlgadgcsomw-bk6w11
Out[2]=2

Visualization  (3)

Visualize the zeroes of BesselJ as a step function:

In[19]:=19
✖
https://wolfram.com/xid/0mlgadgcsomw-g7ixf5
Out[19]=19

Display zeros of the BesselJ function:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-ecj8m7
Out[1]=1

Show the first zero greater than 6:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-df2nos
Out[1]=1

Differentiation and Series Expansions  (5)

Find the derivative of Bessel zero with respect to k:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-oz5ac4
Out[1]=1

Second derivative:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-nfbe0l
Out[1]=1

Find the Taylor expansion using Series:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-ewr1h8
Out[1]=1

Find the series expansion at Infinity:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-syq
Out[1]=1

Taylor expansion at a generic point:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-jwxla7
Out[1]=1

Applications  (3)Sample problems that can be solved with this function

Find the first 10 eigenmodes of a circular drum with Dirichlet boundary conditions:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-jjf5xo
Out[1]=1

Construct an amplitude comprising a certain mixture of modes:

In[2]:=2
✖
https://wolfram.com/xid/0mlgadgcsomw-c8ko17

Circular density plot:

In[3]:=3
✖
https://wolfram.com/xid/0mlgadgcsomw-cfo6eq
Out[3]=3

Radial drum displacement profile:

In[4]:=4
✖
https://wolfram.com/xid/0mlgadgcsomw-6w1r1
Out[4]=4

Find the coefficient in the Rayleigh criterion for diffraction-limited optics:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-gfbw2h
Out[1]=1

Analytically compute the eigenvalues of a Laplacian in Cartesian coordinates over a Disk:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-ukyzsi
Out[1]=1

Properties & Relations  (1)Properties of the function, and connections to other functions

Asymptotic behavior of BesselJZero[ν,k] for large k:

In[1]:=1
✖
https://wolfram.com/xid/0mlgadgcsomw-bgfojp
Out[1]=1
Wolfram Research (2007), BesselJZero, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselJZero.html.
✖
Wolfram Research (2007), BesselJZero, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselJZero.html.

Text

Wolfram Research (2007), BesselJZero, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselJZero.html.

✖
Wolfram Research (2007), BesselJZero, Wolfram Language function, https://reference.wolfram.com/language/ref/BesselJZero.html.

CMS

Wolfram Language. 2007. "BesselJZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BesselJZero.html.

✖
Wolfram Language. 2007. "BesselJZero." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BesselJZero.html.

APA

Wolfram Language. (2007). BesselJZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BesselJZero.html

✖
Wolfram Language. (2007). BesselJZero. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BesselJZero.html

BibTeX

@misc{reference.wolfram_2025_besseljzero, author="Wolfram Research", title="{BesselJZero}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/BesselJZero.html}", note=[Accessed: 18-April-2025 ]}

✖
@misc{reference.wolfram_2025_besseljzero, author="Wolfram Research", title="{BesselJZero}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/BesselJZero.html}", note=[Accessed: 18-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_besseljzero, organization={Wolfram Research}, title={BesselJZero}, year={2007}, url={https://reference.wolfram.com/language/ref/BesselJZero.html}, note=[Accessed: 18-April-2025 ]}

✖
@online{reference.wolfram_2025_besseljzero, organization={Wolfram Research}, title={BesselJZero}, year={2007}, url={https://reference.wolfram.com/language/ref/BesselJZero.html}, note=[Accessed: 18-April-2025 ]}