Binomial

Binomial[n,m]

gives the binomial coefficient TemplateBox[{n, m}, Binomial].

Details

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • Binomial is also known as combinations and as choose function.
  • Binomial gives the symmetric coefficients for negative integer 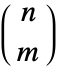. Use PascalBinomial for coefficients that preserve Pascal's identity for all integer values. Binomial and PascalBinomial agree except for negative integer .
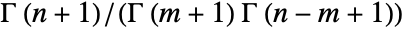  • In general, TemplateBox[{n, m}, Binomial] is defined by (n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma]) or suitable limits of this.
  • When is a negative integer, TemplateBox[{n, m}, Binomial]=TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]. »
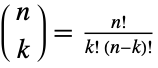  • The particular limit chosen preserves the symmetry rule TemplateBox[{n, m}, Binomial]=TemplateBox[{n, {n, -, m}}, Binomial] for all complex and . »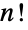
  • Pascal's identity TemplateBox[{n, m}, Binomial]=TemplateBox[{{n, -, 1}, m}, Binomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, Binomial] is satisfied for almost all 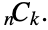and 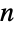, but violated for . »
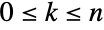  • For integers and certain other special arguments, Binomial automatically evaluates to exact values.
  • Binomial is automatically evaluated symbolically for simple cases; FunctionExpand gives results for other cases. »
  • Binomial can be evaluated to arbitrary numerical precision.
  • Binomial automatically threads over lists.
  • Binomial can be used with Interval and CenteredInterval objects. »

Background & Context

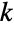  • Binomial represents the binomial coefficient function, which returns the binomial coefficient TemplateBox[{n, k}, Binomial] of and 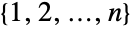. For non-negative integers 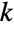and 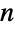, the binomial coefficient has value TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!), where 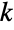is the Factorial function. By symmetry, TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial]. The binomial coefficient is important in probability theory and combinatorics and is sometimes also denoted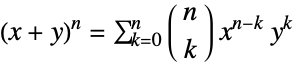
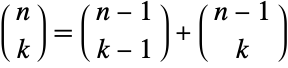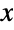  • For non-negative integers and , the binomial coefficient TemplateBox[{n, k}, Binomial] gives the number of subsets of length 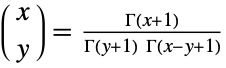contained in the set 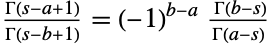. This is also the number of distinct ways of picking elements (without replacement and ignoring order) from the first positive integers and for this reason is often voiced as "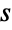 choose ".
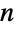  • The binomial coefficient lies at the heart of the binomial formula, which states that for any non-negative integer 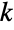, (x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k. This interpretation of binomial coefficients is related to the binomial distribution of probability theory, implemented via BinomialDistribution. Another important application is in the combinatorial identity known as Pascal's rule, which relates the binomial coefficient with shifted arguments according to TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial].
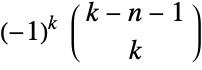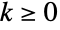  • Expressing factorials as gamma functions generalizes the binomial coefficient to complex and as TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma]). Using the symmetry formula (TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma]) for integer 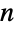and 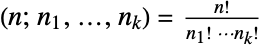and complex 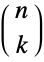then allows the definition of the binomial coefficient to be extended to negative integer arguments, making it continuous at all integer arguments as well as continuous for all complex arguments except for negative integer 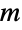and noninteger 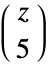(in which case it is infinite). This definition for negative 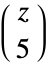and integer 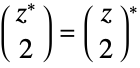, given by (-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial] if 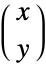, (-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial] if 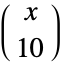and 0 otherwise, is in agreement with both the binomial theorem and most combinatorial identities (with a few special exceptions).
  • Binomial coefficients are generalized by multinomial coefficients. Multinomial returns the multinomial coefficient (n;n1,…,nk) of given numbers n1,…,nk summing to 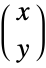, where 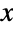. The binomial coefficient TemplateBox[{n, k}, Binomial] is the multinomial coefficient (n;k,n-k).

Examples

open allclose all

Basic Examples  (5)

Evaluate numerically:

Evaluate symbolically:

Construct Pascal's triangle:

Plot over a subset of the reals as a function of its first parameter:

Plot over a subset of the reals as a function of its second parameter:

Plot over a subset of the complexes:

Scope  (35)

Numerical Evaluation  (7)

Evaluate numerically:

Evaluate for half-integer arguments:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix Binomial function using MatrixFunction:

Specific Values  (4)

Values of Binomial at particular points:

Binomial for symbolic n:

Values at zero:

Note that this is zero on all integers away from :

Find a value of n for which Binomial[n,2]=15:

Visualization  (3)

Plot the Binomial as a function of its parameter n:

Plot the Binomial as a function of its parameter :

Plot the real part of TemplateBox[{z, 5}, Binomial]:

Plot the imaginary part of TemplateBox[{z, 5}, Binomial]:

Function Properties  (12)

Real domain of Binomial as a function of its parameter n:

Real domain of Binomial as a function of its parameter m:

Complex domains:

Function range of Binomial:

Binomial has the mirror property TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox], 2}, Binomial]=TemplateBox[{TemplateBox[{z, 2}, Binomial]}, Conjugate]:

Compute sums involving Binomial:

When is positive, TemplateBox[{x, y}, Binomial] is an analytic function of both variables:

This is not true for negative :

TemplateBox[{x, 7}, Binomial] is neither non-decreasing nor non-increasing:

TemplateBox[{x, 7}, Binomial] is not injective:

TemplateBox[{x, 7}, Binomial] is surjective:

Binomial is neither non-negative nor non-positive:

TemplateBox[{x, y}, Binomial] has singularities and discontinuities where is a negative integer:

TemplateBox[{x, 7}, Binomial] is neither convex nor concave:

TraditionalForm formatting:

Differentiation  (3)

First derivative with respect to :

Higher derivatives with respect to :

Plot the higher derivatives with respect to for :

First derivative with respect to :

Series Expansions  (4)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Find the series expansion at Infinity:

Find series expansion for an arbitrary symbolic direction :

Taylor expansion at a generic point:

Function Identities and Simplifications  (2)

Functional identity:

Recurrence relations:

Generalizations & Extensions  (2)

Infinite arguments give symbolic results:

Binomial threads elementwise over lists:

Applications  (11)

There are TemplateBox[{n, m}, Binomial] ways to choose elements without replacements from a set of elements:

Check with direct enumeration:

There are TemplateBox[{{m, +, n, -, 1}, m}, Binomial] ways to choose elements with replacement from a set of elements:

Check with direct enumeration:

There are TemplateBox[{{m, +, n}, m}, Binomial] ways to arrange indistinguishable objects of one kind, and indistinguishable objects of another kind:

Illustrate the binomial theorem:

Fractional binomial theorem:

Binomial coefficients mod 2:

Plot Binomial in the arguments' plane:

Plot the logarithm of the number of ways to pick elements out of :

Compute higher derivatives of a product of two functions:

PDF of the binomial probability distribution:

Bernstein polynomials are defined in terms of Binomial:

Properties & Relations  (11)

On the integers, Binomial[n,m] equals TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]:

This can be expressed as (-1)^m TemplateBox[{{-, n}, m}, Pochhammer]/m! for and (-1)^(n-m) TemplateBox[{{-, n}, {n, -, m}}, Pochhammer]/(n-m)! for :

An alternative formula on the integers:

Pascal's identity is satisfied almost everywhere:

It is violated at the origin:

PascalBinomial satisfies the identity everywhere, including the origin:

The symmetry rule TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial] holds for all values of and :

PascalBinomial performs simple evaluations for symbolic arguments:

For more complex expressions, it will avoid automatic expansion:

Use FunctionExpand with conditions to achieve appropriate simplifications:

Use FullSimplify to simplify expressions involving binomial coefficients:

Use FunctionExpand to expand into Gamma functions:

Sums involving Binomial:

Find the generating function Binomial:

Binomial can be represented as a DifferenceRoot:

The generating function for Binomial:

The exponential generating function for Binomial:

Possible Issues  (3)

Large arguments can give results too large to be computed explicitly:

Machine-number inputs can give high‐precision results:

As a bivariate function, Binomial is not continuous in both variables at negative integers:

The value of Binomial at negative integers is determined via Binomial[n,m]Binomial[n,n-m]:

Neat Examples  (7)

Construct a graphical version of Pascal's triangle:

Extend the triangle to negative integers; unlabeled points indicate a zero value:

PascalBinomial, by contrast, zeroes out the top-left sector where both inputs are negative:

Binomial coefficient mod :

Closed‐form inverse of Hilbert matrices:

Nested binomials over the complex plane:

Plot Binomial at infinity:

Plot Binomial for complex arguments:

Plot Binomial at Gaussian integers:

Wolfram Research (1988), Binomial, Wolfram Language function, https://reference.wolfram.com/language/ref/Binomial.html.

Text

Wolfram Research (1988), Binomial, Wolfram Language function, https://reference.wolfram.com/language/ref/Binomial.html.

CMS

Wolfram Language. 1988. "Binomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Binomial.html.

APA

Wolfram Language. (1988). Binomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Binomial.html

BibTeX

@misc{reference.wolfram_2024_binomial, author="Wolfram Research", title="{Binomial}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Binomial.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_binomial, organization={Wolfram Research}, title={Binomial}, year={1988}, url={https://reference.wolfram.com/language/ref/Binomial.html}, note=[Accessed: 14-November-2024 ]}