Binomial
Binomial[n,m]
二項係数![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学的整数関数である.
- Binomialは,組合せおよび選択関数としても知られている.
- Binomialは,負の整数
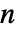 についての対称係数を与える.すべての整数についてパスカル(Pascal)の恒等式を保持する係数についてはPascalBinomialを使う.BinomialおよびPascalBinomialは,負の整数
についての対称係数を与える.すべての整数についてパスカル(Pascal)の恒等式を保持する係数についてはPascalBinomialを使う.BinomialおよびPascalBinomialは,負の整数 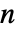 を除いて一致する.
を除いて一致する. - 一般に,
![TemplateBox[{n, m}, Binomial] TemplateBox[{n, m}, Binomial]](Files/Binomial.ja/4.png) は,
は,![(n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma]) (n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma])](Files/Binomial.ja/5.png) またはこの式の適切な極限で定義される.
またはこの式の適切な極限で定義される. 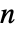 が負の整数のときは,
が負の整数のときは,![TemplateBox[{n, m}, Binomial]=TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip] TemplateBox[{n, m}, Binomial]=TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]](Files/Binomial.ja/7.png) である. »
である. »- 選択された特定の極限が,すべての複素数
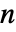 と
と 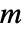 について対称則
について対称則![TemplateBox[{n, m}, Binomial]=TemplateBox[{n, {n, -, m}}, Binomial] TemplateBox[{n, m}, Binomial]=TemplateBox[{n, {n, -, m}}, Binomial]](Files/Binomial.ja/10.png) を保持する. »
を保持する. » - パスカル(Pascal)の恒等式
![TemplateBox[{n, m}, Binomial]=TemplateBox[{{n, -, 1}, m}, Binomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, Binomial] TemplateBox[{n, m}, Binomial]=TemplateBox[{{n, -, 1}, m}, Binomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, Binomial]](Files/Binomial.ja/11.png) は,ほぼすべての
は,ほぼすべての 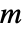 と
と 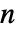 について満足されるが,
について満足されるが,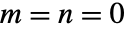 のときは満足されない. »
のときは満足されない. » - 整数およびその他の特別な引数の場合,Binomialは,自動的に厳密値を計算する.
- Binomialは簡単な場合には自動的に記号評価される.その他の場合にはFunctionExpandが結果を与える. »
- Binomialは任意の数値精度で評価できる.
- Binomialは自動的にリストに縫い込まれる.
- BinomialはIntervalオブジェクトおよびCenteredIntervalオブジェクトに使うことができる. »
予備知識
- Binomialは,
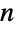 と
と 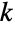 の二項係数
の二項係数![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.ja/17.png) を返す二項係数関数を表す.非負の整数
を返す二項係数関数を表す.非負の整数 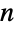 (
(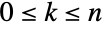 )について,二項係数の値は
)について,二項係数の値は![TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!) TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!)](Files/Binomial.ja/20.png) である.ただし,
である.ただし,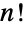 はFactorial関数である.対称性によって
はFactorial関数である.対称性によって![TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial] TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial]](Files/Binomial.ja/22.png) である.二項係数は,確率論や組合せ論において重要である.
である.二項係数は,確率論や組合せ論において重要である.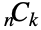 と表記されることがある.
と表記されることがある. - 非負の整数
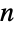 (
(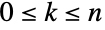 )について,二項係数
)について,二項係数![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.ja/26.png) は,集合
は,集合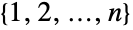 に含まれる長さ
に含まれる長さ 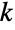 の部分集合の数を与える.これは.最初の
の部分集合の数を与える.これは.最初の 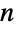 個の整数から
個の整数から 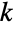 個の元を取り出す(交換は行わず順序は無視した) 重複しない方法の数でもあり,この理由のためにしばしば「
個の元を取り出す(交換は行わず順序は無視した) 重複しない方法の数でもあり,この理由のためにしばしば「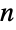 choose
choose 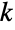 」と発音される.
」と発音される. - 二項係数は,非負の整数
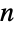 について
について![(x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k (x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k](Files/Binomial.ja/34.png) であるとする二項定理の中心である.二項定理のこの解釈は,BinomialDistributionとして実装されている確率論における二項分布と関連がある.これとは別の重要な応用に,
であるとする二項定理の中心である.二項定理のこの解釈は,BinomialDistributionとして実装されている確率論における二項分布と関連がある.これとは別の重要な応用に,![TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial] TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial]](Files/Binomial.ja/35.png) に従って二項係数をシフトされた引数と関連付ける,パスカルの法則として知られる組合せ恒等式がある.分数をガンマ関数として表現することで二項係数が
に従って二項係数をシフトされた引数と関連付ける,パスカルの法則として知られる組合せ恒等式がある.分数をガンマ関数として表現することで二項係数が![TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma]) TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma])](Files/Binomial.ja/36.png) として複素数
として複素数 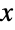 および
および 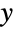 に一般化される.整数
に一般化される.整数 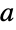 ,
,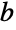 および複素数
および複素数 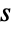 に対称公式
に対称公式![(TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma]) (TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma])](Files/Binomial.ja/42.png) を使い,次に二項係数の定義を負の整数引数まで拡張すると,負の整数
を使い,次に二項係数の定義を負の整数引数まで拡張すると,負の整数 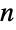 および整数ではない
および整数ではない 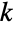 (その場合は不定になる)を除き,二項係数はすべての整数引数および複素引数について連続的となる.
(その場合は不定になる)を除き,二項係数はすべての整数引数および複素引数について連続的となる. 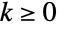 のときは
のときは![(-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial] (-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial]](Files/Binomial.ja/46.png) ,
,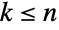 のときは
のときは![(-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial] (-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial]](Files/Binomial.ja/48.png) ,それ以外の場合は0で与えられる負の
,それ以外の場合は0で与えられる負の 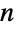 および整数
および整数 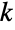 についての定義は,二項定理および(若干の例外が存在するが)ほとんどの組合せ恒等式について成り立つ.
についての定義は,二項定理および(若干の例外が存在するが)ほとんどの組合せ恒等式について成り立つ.- 二項係数は多項係数に一般化される.Multinomialは,合計すると
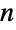 になる与えられた数n1,…,nkの多項係数(n;n1,…,nk)を返す.ただし,
になる与えられた数n1,…,nkの多項係数(n;n1,…,nk)を返す.ただし,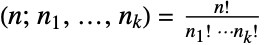 である.二項係数
である.二項係数![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.ja/53.png) は多項係数(n;k,n-k)である.
は多項係数(n;k,n-k)である.
例題
すべて開くすべて閉じる例 (5)
スコープ (35)
数値評価 (7)
IntervalオブジェクトとCenteredIntervalオブジェクトを使って最悪の場合に保証される区間を計算する:
Aroundを使って平均的な場合の統計区間を計算することもできる:
MatrixFunctionを使って行列のBinomial関数を計算することもできる:
特定の値 (4)
関数の特性 (12)
級数展開 (4)
一般化と拡張 (2)
アプリケーション (11)
特性と関係 (11)
整数については,Binomial[n,m]は![]() に等しい:
に等しい:
PascalBinomialは,原点を含む任意の場所で恒等式を満足する:
PascalBinomialは記号引数について簡単な評価を行う:
FunctionExpandを条件とともに使って適切な簡約を行う:
FullSimplifyを使って二項係数を含む式を簡約する:
FunctionExpandを使ってGamma関数に展開する:
Binomialを含む総和:
Binomialの母関数を求める:
BinomialはDifferenceRootとして表すことができる:
Binomialの母関数:
Binomialの指数母関数:
考えられる問題 (3)
おもしろい例題 (7)
三角形を負の整数にまで拡張する.ラベルが付いていない点の値は0である:
これに対し,PascalBinomialは両方の入力が負である左上の部分をゼロにする:
Binomialを無限大でプロットする:
Binomialを複素引数についてプロットする:
Binomialをガウス(Gauss)の整数上でプロットする:
テキスト
Wolfram Research (1988), Binomial, Wolfram言語関数, https://reference.wolfram.com/language/ref/Binomial.html.
CMS
Wolfram Language. 1988. "Binomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Binomial.html.
APA
Wolfram Language. (1988). Binomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Binomial.html