Binomial
Binomial[n,m]
gives the binomial coefficient ![]() .
.
更多信息

- 整数数学函数,适于符号和数值运算.
- Binomial 也称为组合,或称为选择函数.
- Binomial 给出负整数
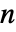 的对称系数. 使用 PascalBinomial 可以得到对所有整数值都保持帕斯卡恒等(Pascal's identity)的系数。除了负整数
的对称系数. 使用 PascalBinomial 可以得到对所有整数值都保持帕斯卡恒等(Pascal's identity)的系数。除了负整数 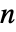 的情况外,Binomial 和 PascalBinomial 是一致的.
的情况外,Binomial 和 PascalBinomial 是一致的. - 通常,
![TemplateBox[{n, m}, Binomial] TemplateBox[{n, m}, Binomial]](Files/Binomial.zh/4.png) 由
由 ![(n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma]) (n!)/(m!(n-m)!)=(TemplateBox[{{n, +, 1}}, Gamma])/(TemplateBox[{{m, +, 1}}, Gamma] TemplateBox[{{n, -, m, +, 1}}, Gamma])](Files/Binomial.zh/5.png) 或适当的极限定义.
或适当的极限定义. - 当
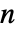 为负整数时,
为负整数时,![TemplateBox[{n, m}, Binomial]=TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip] TemplateBox[{n, m}, Binomial]=TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]](Files/Binomial.zh/7.png) . »
. » - 对于所有复数
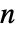 和
和 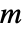 ,所选的特定极限保留了对称规则
,所选的特定极限保留了对称规则 ![TemplateBox[{n, m}, Binomial]=TemplateBox[{n, {n, -, m}}, Binomial] TemplateBox[{n, m}, Binomial]=TemplateBox[{n, {n, -, m}}, Binomial]](Files/Binomial.zh/10.png) . »
. » - 几乎所有
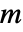 和
和 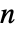 都满足帕斯卡恒等
都满足帕斯卡恒等 ![TemplateBox[{n, m}, Binomial]=TemplateBox[{{n, -, 1}, m}, Binomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, Binomial] TemplateBox[{n, m}, Binomial]=TemplateBox[{{n, -, 1}, m}, Binomial]+TemplateBox[{{n, -, 1}, {m, -, 1}}, Binomial]](Files/Binomial.zh/13.png) ,但
,但 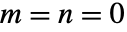 的情况除外. »
的情况除外. » - 对于整数和一些其它特殊参数,Binomial 自动运算出精确值.
- 对简单的情形,自动对 Binomial 进行符号求值;其它情形则由 FunctionExpand 给出结果. »
- Binomial 可求任意数值精度的值.
- Binomial 自动逐项作用于列表的各个元素.
- Binomial 可与 Interval 和 CenteredInterval 对象一起使用. »
背景
- Binomial 表示一个二项式系数函数,返回
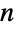 和
和 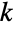 的二项式系数
的二项式系数 ![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.zh/17.png) . 对于非负整数
. 对于非负整数 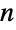 和
和 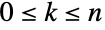 ,二项式系数为
,二项式系数为 ![TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!) TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!)](Files/Binomial.zh/20.png) ,其中
,其中 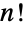 是 Factorial 函数. 通过对称,
是 Factorial 函数. 通过对称,![TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial] TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial]](Files/Binomial.zh/22.png) . 二项式系数在概率论和组合学中很重要,有时被表示为
. 二项式系数在概率论和组合学中很重要,有时被表示为 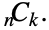
- 对于非负整数
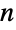 和
和 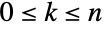 ,二项式系数
,二项式系数 ![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.zh/26.png) 给出包含在集合
给出包含在集合 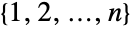 中长度为
中长度为 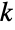 的子集数. 这也是从前
的子集数. 这也是从前 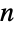 个正整数选择
个正整数选择 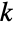 个元素(没有替代和忽略排序)的不同方法数,因此,它常被称之为 "
个元素(没有替代和忽略排序)的不同方法数,因此,它常被称之为 "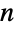 选择
选择 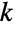 ".
". - 二项式系数位于二项式公式的心脏,它表明对于任何非负整数
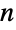 ,
,![(x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k (x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k](Files/Binomial.zh/34.png) . 这种二项式系数的诠释与概率论的二项分布相关,通过 BinomialDistribution 实现. 另一个重要应用是在称之为帕斯卡规则的组合恒等式中,它与根据
. 这种二项式系数的诠释与概率论的二项分布相关,通过 BinomialDistribution 实现. 另一个重要应用是在称之为帕斯卡规则的组合恒等式中,它与根据 ![TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial] TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial]](Files/Binomial.zh/35.png) 带有移位参数的二项系数有关.
带有移位参数的二项系数有关. - 将阶乘表示为伽马函数将二项式系数用
![TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma]) TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma])](Files/Binomial.zh/36.png) 推广为复数
推广为复数 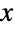 和
和 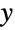 . 对整数
. 对整数 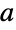 和
和 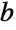 以及复数
以及复数 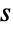 使用对称公式
使用对称公式 ![(TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma]) (TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma])](Files/Binomial.zh/42.png) ,允许二项系数的定义延伸至负整数参数,使其对于所有整数参数以及复数参数是连续的,除了负整数
,允许二项系数的定义延伸至负整数参数,使其对于所有整数参数以及复数参数是连续的,除了负整数 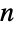 和非整数
和非整数 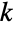 (这种情况下是无穷). 负数
(这种情况下是无穷). 负数 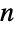 和整数
和整数 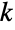 的定义在
的定义在 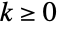 时由
时由 ![(-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial] (-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial]](Files/Binomial.zh/48.png) 给出,在
给出,在 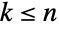 时由
时由 ![(-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial] (-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial]](Files/Binomial.zh/50.png) 给出,否则为 0,这与二项式定理和大多数组合恒等式一致(有一些特殊例外).
给出,否则为 0,这与二项式定理和大多数组合恒等式一致(有一些特殊例外). - 二项式系数通过多项式系数来推广. Multinomial 返回给定数 n1,…,nk 加
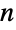 的多项式系数 (n;n1,…,nk),其中
的多项式系数 (n;n1,…,nk),其中 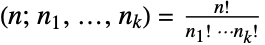 . 二项式系数
. 二项式系数 ![TemplateBox[{n, k}, Binomial] TemplateBox[{n, k}, Binomial]](Files/Binomial.zh/53.png) 是多项式系数 (n;k,n-k).
是多项式系数 (n;k,n-k).
范例
打开所有单元关闭所有单元范围 (35)
数值运算 (7)
用 Interval 和 CenteredInterval 对象计算最坏情况下的区间:
或用 Around 计算一般情况下的统计区间:
或用 MatrixFunction 计算矩阵形式的 Binomial 函数:
特殊值 (4)
函数属性 (12)
推广和延伸 (2)
应用 (11)
属性和关系 (11)
整数情况下,Binomial[n,m] 等于 ![]() :
:
PascalBinomial 在包括原点在内的任何地方都满足恒等:
PascalBinomial 对符号参数进行简单的运算:
使用带条件的 FunctionExpand 来实现适当的化简:
用 FullSimplify 简化含有二项式系数的表达式:
用 FunctionExpand 将二项式系数展开为 Gamma 函数:
含有 Binomial 的求和:
求母函数 Binomial:
Binomial 可被表示为 DifferenceRoot:
Binomial 的母函数:
Binomial 的指数母函数:
可能存在的问题 (3)
巧妙范例 (7)
构建帕斯卡三角形(Pascal's triangle)的图形版本:
相比之下,在输入均为负数的情况下,PascalBinomial 导致左上角的扇形区域为零:
绘制无穷处的 Binomial:
绘制自变量为复数的 Binomial :
绘制自变量为高斯整数的 Binomial:
文本
Wolfram Research (1988),Binomial,Wolfram 语言函数,https://reference.wolfram.com/language/ref/Binomial.html.
CMS
Wolfram 语言. 1988. "Binomial." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/Binomial.html.
APA
Wolfram 语言. (1988). Binomial. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Binomial.html 年