BirnbaumImportance
✖
BirnbaumImportance
更多信息
- BirnbaumImportance 也称为可靠性重要度.
- Birnbaum 重要度通过将故障组分
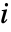 用完美组分
用完美组分  替换使可靠性得以改善.
替换使可靠性得以改善. - 组分
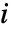 在时刻
在时刻  的 Birnbaum 重要度为
的 Birnbaum 重要度为  ,其中
,其中 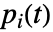 是已知第
是已知第  个组分完美的条件下系统工作的概率,
个组分完美的条件下系统工作的概率,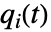 是第
是第 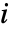 个组分出现故障的条件下系统工作的概率.
个组分出现故障的条件下系统工作的概率. - 返回的结果按照 rdist 或 fdist 中所列分布的次序给出.
范例
打开所有单元关闭所有单元基本范例 (3)常见实例总结
https://wolfram.com/xid/0bsxqckh9twewpyxsy-e66rb
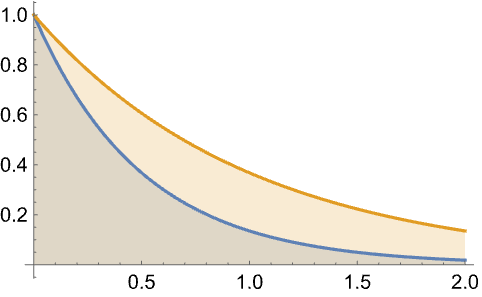
结果按照 ReliabilityDistribution 中的分布列表次序给出:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-4wtin8
https://wolfram.com/xid/0bsxqckh9twewpyxsy-d43v3q
https://wolfram.com/xid/0bsxqckh9twewpyxsy-yn943z
https://wolfram.com/xid/0bsxqckh9twewpyxsy-8e7d7o
https://wolfram.com/xid/0bsxqckh9twewpyxsy-28utav
https://wolfram.com/xid/0bsxqckh9twewpyxsy-fmkne5
https://wolfram.com/xid/0bsxqckh9twewpyxsy-0zv592
范围 (17)标准用法实例范围调查
可靠性分布模型 (9)
https://wolfram.com/xid/0bsxqckh9twewpyxsy-08flls
https://wolfram.com/xid/0bsxqckh9twewpyxsy-mkns50
https://wolfram.com/xid/0bsxqckh9twewpyxsy-rwabaw
https://wolfram.com/xid/0bsxqckh9twewpyxsy-f1wvq8
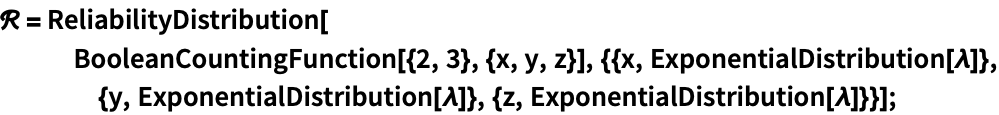
https://wolfram.com/xid/0bsxqckh9twewpyxsy-mji74e
https://wolfram.com/xid/0bsxqckh9twewpyxsy-xc5531
https://wolfram.com/xid/0bsxqckh9twewpyxsy-bs7f7v
https://wolfram.com/xid/0bsxqckh9twewpyxsy-jy1k7y
https://wolfram.com/xid/0bsxqckh9twewpyxsy-6vuxir
https://wolfram.com/xid/0bsxqckh9twewpyxsy-fn2idk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-8pfw08
https://wolfram.com/xid/0bsxqckh9twewpyxsy-mjkl5o
https://wolfram.com/xid/0bsxqckh9twewpyxsy-t1mcxq
https://wolfram.com/xid/0bsxqckh9twewpyxsy-xfjq50
https://wolfram.com/xid/0bsxqckh9twewpyxsy-3daofy
https://wolfram.com/xid/0bsxqckh9twewpyxsy-lqd3ci
https://wolfram.com/xid/0bsxqckh9twewpyxsy-srbs5o

https://wolfram.com/xid/0bsxqckh9twewpyxsy-xwt0s4
https://wolfram.com/xid/0bsxqckh9twewpyxsy-pr0k1j
https://wolfram.com/xid/0bsxqckh9twewpyxsy-bkyutz
https://wolfram.com/xid/0bsxqckh9twewpyxsy-urftd7
https://wolfram.com/xid/0bsxqckh9twewpyxsy-vf85i0
https://wolfram.com/xid/0bsxqckh9twewpyxsy-4n9ka6
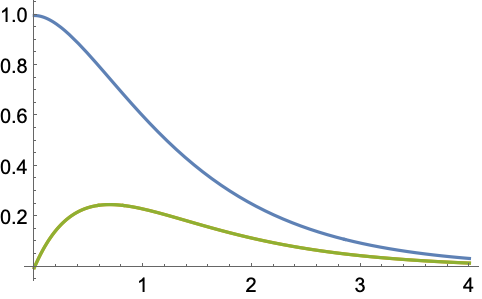
可以使用任何有效的 ReliabilityDistribution:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-cjmrsj
https://wolfram.com/xid/0bsxqckh9twewpyxsy-6zfypk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-6lxtrj
https://wolfram.com/xid/0bsxqckh9twewpyxsy-iedm9b
https://wolfram.com/xid/0bsxqckh9twewpyxsy-dcrxnl
https://wolfram.com/xid/0bsxqckh9twewpyxsy-2f3o3y
https://wolfram.com/xid/0bsxqckh9twewpyxsy-n8cikq
https://wolfram.com/xid/0bsxqckh9twewpyxsy-kf0c4n
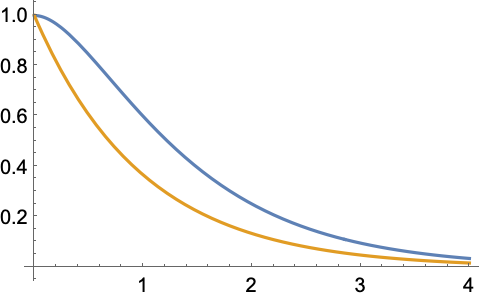
失效分布模型 (8)
https://wolfram.com/xid/0bsxqckh9twewpyxsy-l11ptk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-6nc5zk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-xmgcyf
https://wolfram.com/xid/0bsxqckh9twewpyxsy-nlxcpv
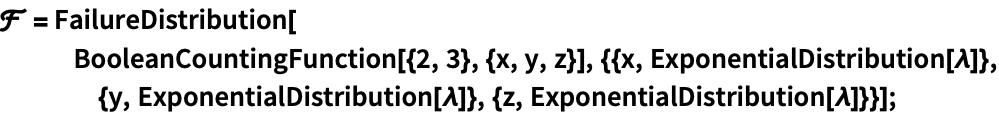
https://wolfram.com/xid/0bsxqckh9twewpyxsy-natpec
https://wolfram.com/xid/0bsxqckh9twewpyxsy-xz9lrc
https://wolfram.com/xid/0bsxqckh9twewpyxsy-4jsp53
https://wolfram.com/xid/0bsxqckh9twewpyxsy-3a7nr5
https://wolfram.com/xid/0bsxqckh9twewpyxsy-wh2s2m
https://wolfram.com/xid/0bsxqckh9twewpyxsy-tynywc
https://wolfram.com/xid/0bsxqckh9twewpyxsy-fecls
https://wolfram.com/xid/0bsxqckh9twewpyxsy-sr2e4s
https://wolfram.com/xid/0bsxqckh9twewpyxsy-gbr67k
https://wolfram.com/xid/0bsxqckh9twewpyxsy-88i8fa
https://wolfram.com/xid/0bsxqckh9twewpyxsy-ig97mn
https://wolfram.com/xid/0bsxqckh9twewpyxsy-xdjp3g
https://wolfram.com/xid/0bsxqckh9twewpyxsy-4smvi5

https://wolfram.com/xid/0bsxqckh9twewpyxsy-pcd9ai
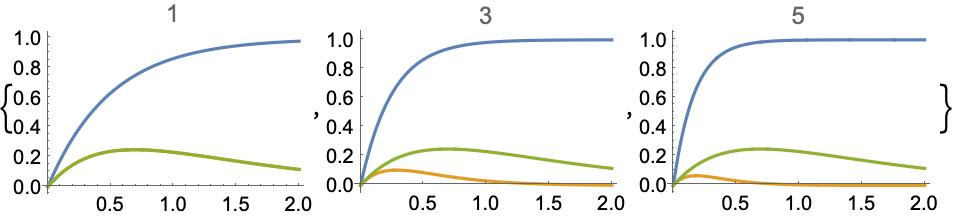
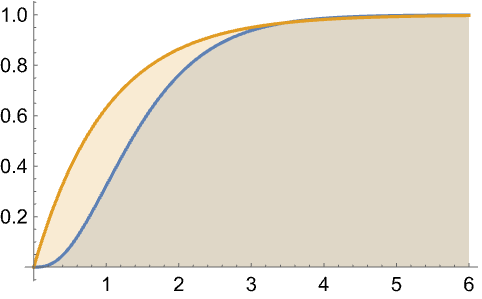
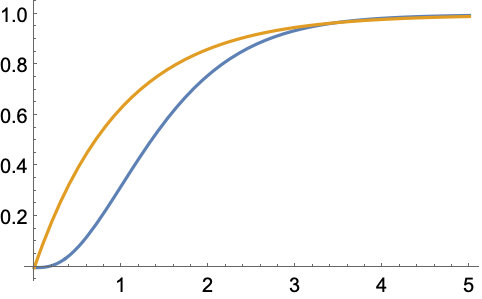
可以使用任何有效的 FailureDistribution:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-34mp4o
https://wolfram.com/xid/0bsxqckh9twewpyxsy-i1m9g0
https://wolfram.com/xid/0bsxqckh9twewpyxsy-9qepae
https://wolfram.com/xid/0bsxqckh9twewpyxsy-cmc5tk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-lxyr6j
https://wolfram.com/xid/0bsxqckh9twewpyxsy-mvuep3
https://wolfram.com/xid/0bsxqckh9twewpyxsy-okc513
https://wolfram.com/xid/0bsxqckh9twewpyxsy-5ll2fu
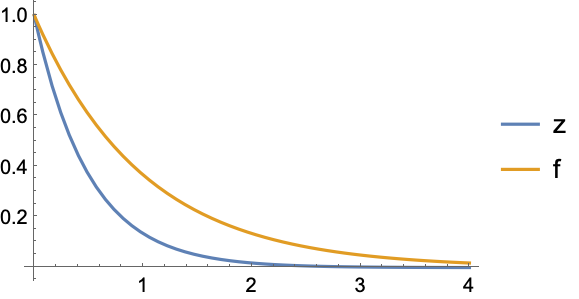
应用 (5)用该函数可以解决的问题范例
https://wolfram.com/xid/0bsxqckh9twewpyxsy-bqrgiq
https://wolfram.com/xid/0bsxqckh9twewpyxsy-wgnax0
https://wolfram.com/xid/0bsxqckh9twewpyxsy-ud0au2
https://wolfram.com/xid/0bsxqckh9twewpyxsy-7l5tir
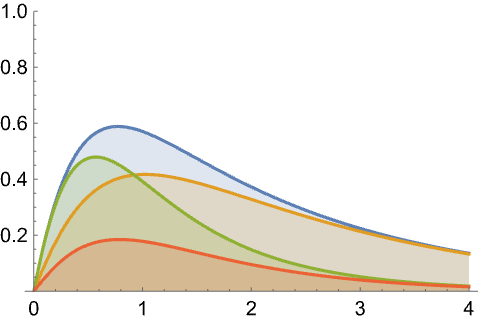
对于一个任务时间为3个小时的系统,改进组分 x 将使系统得到最大改进:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-k1mgn7
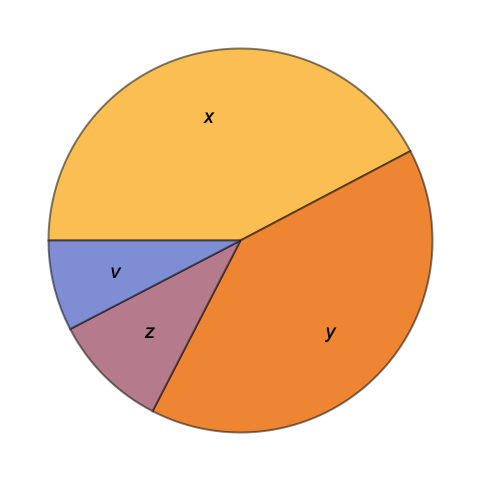
研究由一个组分串联且两个组分并联的系统. 根据 Birnbaum 重要度确定最重要的组分:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-px940y
https://wolfram.com/xid/0bsxqckh9twewpyxsy-r7aaoz
https://wolfram.com/xid/0bsxqckh9twewpyxsy-z0lrx3
https://wolfram.com/xid/0bsxqckh9twewpyxsy-vh5o5o
https://wolfram.com/xid/0bsxqckh9twewpyxsy-o42yzk
https://wolfram.com/xid/0bsxqckh9twewpyxsy-exmlhu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-b1at50
https://wolfram.com/xid/0bsxqckh9twewpyxsy-cytpg1
https://wolfram.com/xid/0bsxqckh9twewpyxsy-wdz6a0
https://wolfram.com/xid/0bsxqckh9twewpyxsy-oqtwlm
https://wolfram.com/xid/0bsxqckh9twewpyxsy-mef539
https://wolfram.com/xid/0bsxqckh9twewpyxsy-evcow9
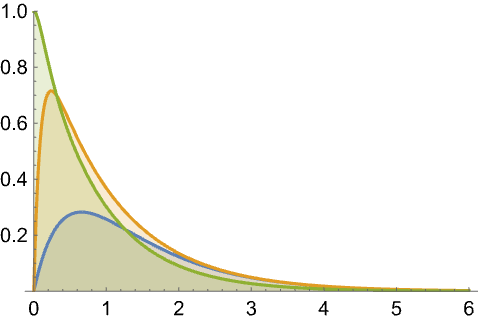
改进组分 ![]() 效果最佳. 改善组分
效果最佳. 改善组分 ![]() 比改善组分
比改善组分![]() 更符合成本效益:
更符合成本效益:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-elyj2o
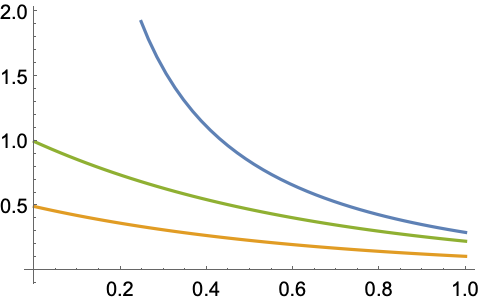
城市两点之间由一个水管 ![]() 组成的网络相连. 求对保证供水最关键的管道:
组成的网络相连. 求对保证供水最关键的管道:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-d08rnu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-r3su1o
https://wolfram.com/xid/0bsxqckh9twewpyxsy-kmt3or
https://wolfram.com/xid/0bsxqckh9twewpyxsy-ji6eio
https://wolfram.com/xid/0bsxqckh9twewpyxsy-uemvn8
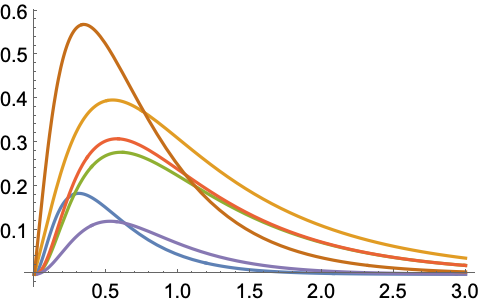
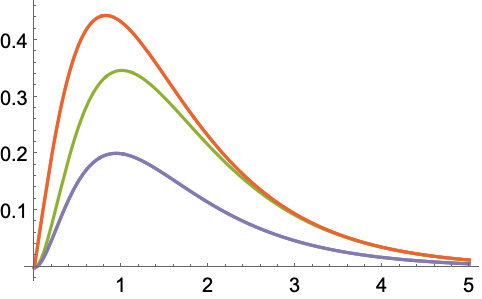
对于五个泵的石油管道系统,如果不多于两个连续泵出现故障,则管道系统将正常工作. 找到最重要的泵:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-2qi6zi
https://wolfram.com/xid/0bsxqckh9twewpyxsy-qxfyu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-5uxb2l
属性和关系 (6)函数的属性及与其他函数的关联
BirnbaumImportance 可以用概率的形式定义:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-h5mvwn
https://wolfram.com/xid/0bsxqckh9twewpyxsy-gdczdm
https://wolfram.com/xid/0bsxqckh9twewpyxsy-lac9wy
https://wolfram.com/xid/0bsxqckh9twewpyxsy-crj1mx
https://wolfram.com/xid/0bsxqckh9twewpyxsy-8wr007
CriticalityFailureImportance 与 BirnbaumImportance 有关:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-hwswhu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-rdk742
https://wolfram.com/xid/0bsxqckh9twewpyxsy-b29d79
https://wolfram.com/xid/0bsxqckh9twewpyxsy-b3nojy
与 CriticalityFailureImportance 的定义比较:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-kt65u7
ImprovementImportance 与 BirnbaumImportance 有关:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-2uwhqu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-5hmaxc
https://wolfram.com/xid/0bsxqckh9twewpyxsy-hqhhkl
https://wolfram.com/xid/0bsxqckh9twewpyxsy-0rzj3t
与 ImprovementImportance 的定义比较:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-caz8bu
https://wolfram.com/xid/0bsxqckh9twewpyxsy-zn9d03
https://wolfram.com/xid/0bsxqckh9twewpyxsy-m1491r
https://wolfram.com/xid/0bsxqckh9twewpyxsy-g2591
https://wolfram.com/xid/0bsxqckh9twewpyxsy-qx43x6
https://wolfram.com/xid/0bsxqckh9twewpyxsy-kvr29j
StructuralImportance 是组分可靠性为 ![]() 的 Birnbaum 重要度:
的 Birnbaum 重要度:
https://wolfram.com/xid/0bsxqckh9twewpyxsy-bjyuku
https://wolfram.com/xid/0bsxqckh9twewpyxsy-k1oaw5
https://wolfram.com/xid/0bsxqckh9twewpyxsy-q7t7kn
https://wolfram.com/xid/0bsxqckh9twewpyxsy-cwsfzm
https://wolfram.com/xid/0bsxqckh9twewpyxsy-hj41uj
Wolfram Research (2012),BirnbaumImportance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BirnbaumImportance.html.文本
Wolfram Research (2012),BirnbaumImportance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BirnbaumImportance.html.
Wolfram Research (2012),BirnbaumImportance,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BirnbaumImportance.html.CMS
Wolfram 语言. 2012. "BirnbaumImportance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BirnbaumImportance.html.
Wolfram 语言. 2012. "BirnbaumImportance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/BirnbaumImportance.html.APA
Wolfram 语言. (2012). BirnbaumImportance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BirnbaumImportance.html 年
Wolfram 语言. (2012). BirnbaumImportance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BirnbaumImportance.html 年BibTeX
@misc{reference.wolfram_2025_birnbaumimportance, author="Wolfram Research", title="{BirnbaumImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BirnbaumImportance.html}", note=[Accessed: 13-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_birnbaumimportance, organization={Wolfram Research}, title={BirnbaumImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/BirnbaumImportance.html}, note=[Accessed: 13-April-2025
]}