BiweightLocation

BiweightLocation[list]

list 中の要素のバイウェイト位置推定器の値を与える．

BiweightLocation[list,c]

尺度母数が c のバイウェイト位置推定器の値を与える．

詳細とオプション

  • BiweightLocationはロバストな位置推定器である．
  • BiweightLocationは要素の重み付き平均によって与えられる．中心から遠い要素ほど重みが小さい．
  • 重み関数の幅尺度は母数 c によって制御される．大きい c は統計計算により多くのデータ値が含まれることを意味し，逆もまた真である．
  • リスト{x1,x2,…,xn}について，バイウェイト位置推定器の値は で与えられる．ただし，であり 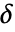はMedian[{x1-x*,x2-x*,…,xn-x*}]である．推定器の値 x*は，デフォルトで自動的に選択された初期値を使って反復的に計算される．
  • BiweightLocation[list]はBiweightLocation[list,6]に等しい．
  • BiweightLocation[{{x1,y1,…},{x2,y2,…},…}]は{BiweightLocation[{x1,x2,…}],BiweightLocation[{y1,y2,…}],…}を与える．
  • BiweightLocationでは c は任意の正の実数でよい．
  • 次は使用可能なオプションである．
  • AccuracyGoalAutomatic目標確度
    MaxIterations Automatic使用する最大反復回数
    Method Automatic使用するメソッド
    PrecisionGoalAutomatic目標精度
    WorkingPrecisionMachinePrecision内部計算に使用される精度
  • Method{"InitialPoint"x0}の設定でカスタム初期値 を使うことができる．

例題

すべて開くすべて閉じる

例  (4)

リストのBiweightLocation：

行列の列のBiweightLocation：

尺度母数が7のリストのBiweightLocation：

日付のリストのBiweightLocation：

スコープ  (8)

精度が異なる同じ入力：

尺度母数が異なるバイウェイト位置：

行列についてのバイウェイト位置は列ごとの推定を与える：

大きい配列のバイウェイト位置：

TimeSeriesのバイウェイト位置を求める：

バイウェイト位置は値のみに依存する：

バイウェイト位置は，単位付き数量を含むデータに使うことができる：

日付のバイウェイト位置を計算する：

時間のバイウェイト位置を計算する：

異なる時刻帯指定の時刻のリスト：

オプション  (2)

MaxIterations  (1)

BiweightLocationの値は反復的に計算される．計算で試みられる反復回数を制限する：

Method  (1)

BiweightLocationの計算で初期値を調整する：

よりよい初期値を使い，反復回数を制限する：

アプリケーション  (3)

外れ値がある場合の位置のロバスト推定を得る：

極値はMeanに大きく影響する：

ガウスの混合分布からのデータについて考察する：

Meanで中心を推定する：

サンプル平均推定器はガウス分布に従わないデータについては大きく広がる．推定器の標準偏差は以下の通りである：

BiweightLocationで中心を推定する：

ブートストラップ法を使ってバイウェイト位置推定器の広がりを見積もる：

裾の重い測定ノイズのある軌跡のシミュレーションを行う：

もとになっている信号とノイズがあるシミュレーション結果の経路：

移動BiweightLocationを使って軌跡を平滑化する：

ブロックサイズを大きくすると軌跡がより滑らかになる：

特性と関係  (3)

サンプルのバイウェイト位置を計算する：

区間外の値は統計に影響しない．ただし，はバイウェイト位置の値， は についての中央値絶対偏差， はデフォルト値が6に等しい尺度母数である：

バイウェイト位置の計算に使われている重み関数 w(x)の形：

サンプル中の最大値と最小値を2倍してバイウェイト位置を再び計算する：

正規分布に従うサンプルについては，BiweightLocationとMeanはほぼ等しい：

CauchyDistributionからのデータのように正規分布に従わないサンプルについては，BiweightLocationは中心位置についてMeanよりよい推定を与える：

BiweightLocationは，c の大きい値についてはMeanに近付く：

おもしろい例題  (2)

尺度係数 c に依存する一変量データの平均周囲のバイウェイト位置の変化：

尺度係数 c に依存する二変量データの平均周囲のバイウェイト位置の変化：

Wolfram Research (2017), BiweightLocation, Wolfram言語関数， https://reference.wolfram.com/language/ref/BiweightLocation.html （2024年に更新）.

テキスト

Wolfram Research (2017), BiweightLocation, Wolfram言語関数， https://reference.wolfram.com/language/ref/BiweightLocation.html （2024年に更新）.

CMS

Wolfram Language. 2017. "BiweightLocation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/BiweightLocation.html.

APA

Wolfram Language. (2017). BiweightLocation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BiweightLocation.html

BibTeX

@misc{reference.wolfram_2024_biweightlocation, author="Wolfram Research", title="{BiweightLocation}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/BiweightLocation.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_biweightlocation, organization={Wolfram Research}, title={BiweightLocation}, year={2024}, url={https://reference.wolfram.com/language/ref/BiweightLocation.html}, note=[Accessed: 21-November-2024 ]}