BiweightLocation
BiweightLocation[list]
给出 list 中元素的双权位置估计量的值.
BiweightLocation[list,c]
给出缩放参数为 c 的双权位置估计量的值.
更多信息和选项

- BiweightLocation 是稳健的位置估计量.
- BiweightLocation 由元素的加权均值给出. 离中心较远的元素的权重也较低.
- 加权函数的宽度由参数 c 控制. 较大的 c 表明在计算统计量时有更多的数据被包含进来,反之亦然.
- 对于列表 {x1,x2,…,xn} ,双权位置估计量的值由
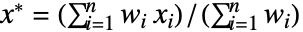 给出,其中
给出,其中 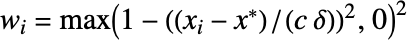 ,
,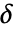 为 Median[{x1-x*,x2-x*,…,xn-x*}]. 以迭代式计算估计量的值 x* ,缺省情况下自动选择初值.
为 Median[{x1-x*,x2-x*,…,xn-x*}]. 以迭代式计算估计量的值 x* ,缺省情况下自动选择初值. - BiweightLocation[list] 等价于 BiweightLocation[list,6].
- BiweightLocation[{{x1,y1,…},{x2,y2,…},…}] 给出 {BiweightLocation[{x1,x2,…}],BiweightLocation[{y1,y2,…}],…}.
- BiweightLocation 允许 c 为任意正实数.
- 可以给出下列选项:
-
AccuracyGoal Automatic 寻求的准确度 MaxIterations Automatic 使用的最大迭代次数 Method Automatic 使用的方法 PrecisionGoal Automatic 寻求的精度 WorkingPrecision MachinePrecision 内部计算中使用的精度 - 设置 Method{"InitialPoint"x0} 允许自定义初值
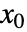 .
.
范例
打开所有单元关闭所有单元基本范例 (4)
列表的 BiweightLocation:
矩阵的列的 BiweightLocation:
缩放参数为 7 时列表的 BiweightLocation :
日期列表的 BiweightLocation:
范围 (8)
求 TimeSeries 的双权位置:
选项 (2)
MaxIterations (1)
BiweightLocation 的值是迭代式算出的. 限制计算时迭代的次数:
Method (1)
应用 (3)
极值对 Mean 的影响较大:
用 Mean 估计中心:
对于非高斯分布数据,样本均值估计量有较大的展布 (spread). 估计量的标准偏差为:
用 BiweightLocation 来估计中心:
用移动 BiweightLocation 平滑轨迹:
属性和关系 (3)
区间 ![]() 之外的值对统计量没有影响. 这里
之外的值对统计量没有影响. 这里 ![]() 是双权位置的值,
是双权位置的值,![]() 是关于
是关于 ![]() 的绝对中位差.
的绝对中位差. ![]() 是缩放参数,默认值为 6:
是缩放参数,默认值为 6:
对于正态分布的样本,BiweightLocation 和 Mean 几乎相等:
对于非正态分布的样本,如来自 CauchyDistribution 的数据,BiweightLocation 给出的中心位置的估计比 Mean 给出的要更好:
当 c 取较大值时,BiweightLocation 接近 Mean:
文本
Wolfram Research (2017),BiweightLocation,Wolfram 语言函数,https://reference.wolfram.com/language/ref/BiweightLocation.html (更新于 2024 年).
CMS
Wolfram 语言. 2017. "BiweightLocation." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/BiweightLocation.html.
APA
Wolfram 语言. (2017). BiweightLocation. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/BiweightLocation.html 年