ConjugateTranspose
または ![]() は,
は,![]() の共役転置を与える.
の共役転置を与える.
詳細とオプション
- ConjugateTranspose[m]はConjugate[Transpose[m]]と等価である. »
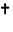 は,
は, ct
ct あるいは\[ConjugateTranspose]として入力できる.
あるいは\[ConjugateTranspose]として入力できる.- ConjugateTranspose[m]は
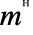 として与えることもできる.
として与えることもできる. は
は hc
hc あるいは\[HermitianConjugate]として入力できる.
あるいは\[HermitianConjugate]として入力できる. - ConjugateTranspose[m,spec]はConjugate[Transpose[m,spec]]を返す.
例題
すべて開くすべて閉じるスコープ (12)
行列 (7)
ConjugateTranspose[vec]は項を共役するが vec の形状は変えない:
ConjugateTransposeは記号行列に使うことができる:
ComplexExpandを使ってすべての変数が実数であると仮定する:
ConjugateTransposeは恒等行列は変えずに置く:
SymmetrizedArrayオブジェクトを転置する:
行列は反対称行列なので,結果はもとのオブジェクトを負にしたものである:
TraditionalFormによる記号共役転置をフォーマットする:
配列 (5)
3階配列の最初の2つのレベルの共役転置は,事実上,この配列をベクトルの行列として扱う:
TwoWayRule表記を使って転置を行う:
アプリケーション (10)
行列分解 (4)
![]() のQRDecompositionを求める:
のQRDecompositionを求める:
行列 ![]() のSchurDecompositionを計算する:
のSchurDecompositionを計算する:
行列 ![]() のSingularValueDecompositionを計算する:
のSingularValueDecompositionを計算する:
特殊行列 (6)
エルミート行列は ![]() に従い,反エルミート行列は
に従い,反エルミート行列は ![]() に従う.次の行列はエルミート行列である:
に従う.次の行列はエルミート行列である:
HermitianMatrixQで確認する:
AntihermitianMatrixQで確認する:
![]() なら行列はユニタリ行列である.行列
なら行列はユニタリ行列である.行列 ![]() がユニタリ行列かどうかを調べる:
がユニタリ行列かどうかを調べる:
UnitaryMatrixQを使ってこれがユニタリ行列であることを確認する:
エルミート行列は ![]() のようにユニタリ対角化可能である.ただし,
のようにユニタリ対角化可能である.ただし,![]() は実対角行列では
は実対角行列では ![]() はユニタリ行列である.次の行列がエルミート行列であることを確認し,次にこれを対角化する:
はユニタリ行列である.次の行列がエルミート行列であることを確認し,次にこれを対角化する:
対角化するために,まず ![]() の固有値を計算し,それを対角行列に入れる:
の固有値を計算し,それを対角行列に入れる:
反エルミート行列は, ![]() なのでユニタリ対角化可能である.ただし,
なのでユニタリ対角化可能である.ただし,![]() は複素対角行列で
は複素対角行列で ![]() はユニタリ行列である.次の行列が反エルミート行列であることを確認して対角化する:
はユニタリ行列である.次の行列が反エルミート行列であることを確認して対角化する:
対角化するために,まず ![]() の固有値を計算し,それを対角行列に入れる:
の固有値を計算し,それを対角行列に入れる:
ユニタリ行列はそれ自体が ![]() のようにユニタリ対角化可能である.ただし,
のようにユニタリ対角化可能である.ただし,![]() はユニタリ行列で
はユニタリ行列で ![]() は単位円上にある項を持つ対角行列である.次の行列がユニタリ行列であることを確認して対角化する:
は単位円上にある項を持つ対角行列である.次の行列がユニタリ行列であることを確認して対角化する:
![]() なら行列
なら行列 ![]() は正規行列と呼ばれる.正規行列は,
は正規行列と呼ばれる.正規行列は,![]() (
(![]() は対角行列で
は対角行列で ![]() はユニタリ行列)のようにユニタリ対角化可能である最も一般的な行列である.エルミート行列
はユニタリ行列)のようにユニタリ対角化可能である最も一般的な行列である.エルミート行列 ![]() は,等式の両辺が単純に
は,等式の両辺が単純に ![]() なので,どれも正規行列である:
なので,どれも正規行列である:
同様に,反エルミート行列は,等式の両辺が単純に![]() なので,すべて正規行列である:
なので,すべて正規行列である:
ユニタリ行列は,定義 ![]() に代入すると両辺に恒等行列が与えられるので,正規行列である:
に代入すると両辺に恒等行列が与えられるので,正規行列である:
NormalMatrixQを使って確認する:
![]() のような正規行列はEigensystemを使ってユニタリ対角化できる:
のような正規行列はEigensystemを使ってユニタリ対角化できる:
特性と関係 (10)
ConjugateTranspose[m]はConjugate[Transpose[m]]に等しい:
ConjugateTransposeは![]() に従う:
に従う:
互換行列 ![]() と
と ![]() についてConjugateTransposeは
についてConjugateTransposeは![]() に従う:
に従う:
行列の反転はConjugateTransposeと可換である.すなわち![]() :
:
特殊行列の多くはConjugateTransposeのもとの特性で定義される.エルミート行列は ![]() という特性を持つ:
という特性を持つ:
次元{1,0}の置換は{0,1}で次元{0,1}の式はないので,結果は再度{{}}にはならない:
ConjugateTranspose[a]は配列の最初の2レベルを転置する:
ConjugateTranspose[a,perm]は次元Permute[Dimensions[a],perm]の配列を返す:
テキスト
Wolfram Research (2004), ConjugateTranspose, Wolfram言語関数, https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
CMS
Wolfram Language. 2004. "ConjugateTranspose." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
APA
Wolfram Language. (2004). ConjugateTranspose. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConjugateTranspose.html