ConjugateTranspose
或 ![]() ,给出
,给出 ![]() 的共轭转置.
的共轭转置.
更多信息和选项
- ConjugateTranspose[m] 等价于 Conjugate[Transpose[m]]. »
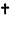 可以通过输入
可以通过输入  ct
ct 或 \[ConjugateTranspose] 得到.
或 \[ConjugateTranspose] 得到. - ConjugateTranspose[m] 也可以作为
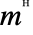 给出,其中
给出,其中 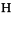 通过输入
通过输入  hc
hc 或\[HermitianConjugate] 得到.
或\[HermitianConjugate] 得到. - ConjugateTranspose[m,spec] 给出 Conjugate[Transpose[m,spec]].
范例
打开所有单元关闭所有单元范围 (12)
矩阵 (7)
ConjugateTranspose[vec] 对项进行共轭,但不会改变 vec 的形状:
ConjugateTranspose 适用于符号矩阵:
使用 ComplexExpand 假设所有变量都是实数:
ConjugateTranspose 保持单位矩阵不变:
转置一个 SymmetrizedArray 对象:
在 TraditionalForm 中格式化一个符号共轭转置:
数组 (5)
对秩为 3 的数组的前两层进行共轭转置,有效地将其视为向量矩阵:
使用 TwoWayRule 表示法进行转置:
应用 (10)
矩阵分解 (4)
特数矩阵 (6)
埃尔米特矩阵服从 ![]() ,反埃尔米矩阵服从
,反埃尔米矩阵服从 ![]() . 该矩阵为埃尔米特矩阵:
. 该矩阵为埃尔米特矩阵:
使用 HermitianMatrixQ 进行验证:
使用 AntihermitianMatrixQ 进行验证:
使用 UnitaryMatrixQ 验证酉矩阵:
埃尔米特矩阵可酉对角化为 ![]() ,其中
,其中 ![]() 为是对角实数矩阵,
为是对角实数矩阵,![]() 为酉矩阵. 验证以下矩阵是埃尔米特矩阵,然后对其进行对角化:
为酉矩阵. 验证以下矩阵是埃尔米特矩阵,然后对其进行对角化:
反埃尔米特阵可酉对角化为 ![]() ,其中
,其中 ![]() 为对角矩阵且值为虚数,
为对角矩阵且值为虚数,![]() 为酉矩阵. 验证以下矩阵是反埃尔米矩阵,然后对其进行对角化:
为酉矩阵. 验证以下矩阵是反埃尔米矩阵,然后对其进行对角化:
酉矩阵本身可酉对角化为 ![]() ,其中
,其中 ![]() 为酉矩阵且
为酉矩阵且 ![]() 为对角矩阵,其项位于单位圆上. 验证以下矩阵是酉矩阵,然后对其进行对角化:
为对角矩阵,其项位于单位圆上. 验证以下矩阵是酉矩阵,然后对其进行对角化:
如果 ![]() ,则矩阵
,则矩阵 ![]() 被称为正规矩阵. 正规矩阵是最通用的一种矩阵,它可以被酉对角化为
被称为正规矩阵. 正规矩阵是最通用的一种矩阵,它可以被酉对角化为 ![]() ,其中
,其中 ![]() 为对角矩阵,且
为对角矩阵,且 ![]() 为酉矩阵. 所有埃尔米特矩阵
为酉矩阵. 所有埃尔米特矩阵 ![]() 都是正规的,因为等式的两边都只是
都是正规的,因为等式的两边都只是 ![]() :
:
酉矩阵是正规矩阵,因为在定义中代入 ![]() 会在等式两边给出单位矩阵:
会在等式两边给出单位矩阵:
使用 NormalMatrixQ 进行验证:
像 ![]() 这样的正规矩阵可使用 Eigensystem 进行酉对角化:
这样的正规矩阵可使用 Eigensystem 进行酉对角化:
属性和关系 (10)
ConjugateTranspose[m] 等价于 Conjugate[Transpose[m]]:
ConjugateTranspose 服从 ![]() :
:
对于兼容矩阵 ![]() 和
和 ![]() ,ConjugateTranspose 服从
,ConjugateTranspose 服从 ![]() :
:
矩阵求逆与 ConjugateTranspose 互换,即 ![]() :
:
许多特殊矩阵根据其在 ConjugateTranspose 下的属性进行定义. 埃尔米特矩阵有 ![]() :
:
结果不能再次为 {{}} ,因为维度 {1,0} 的排列是 {0,1} 且没有表达式有维度 {0,1}:
ConjugateTranspose[a] 转置数组的前两层:
ConjugateTranspose[a,perm] 返回维数为 Permute[Dimensions[a],perm] 的数组:
文本
Wolfram Research (2004),ConjugateTranspose,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
CMS
Wolfram 语言. 2004. "ConjugateTranspose." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ConjugateTranspose.html.
APA
Wolfram 语言. (2004). ConjugateTranspose. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ConjugateTranspose.html 年