ConvexHullMesh

ConvexHullMesh[{p1,p2,…}]

gives a BoundaryMeshRegion representing the convex hull from the points p1, p2, ….

ConvexHullMesh[mreg]

gives the convex hull of the mesh region mreg.

Details and Options

  • ConvexHullMesh is also known as convex envelope or convex closure.
  • The convex hull mesh is the smallest convex set that includes the points pi.
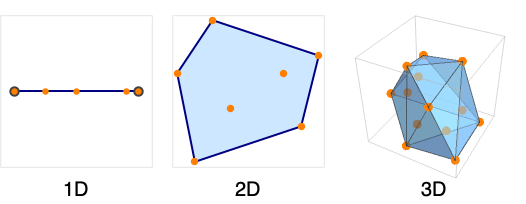
  • The convex hull boundary consists of points in 1D, line segments in 2D, and convex polygons in 3D.
  • ConvexHullMesh takes the same options as BoundaryMeshRegion.

Examples

open allclose all

Basic Examples  (3)

A 1D convex hull mesh:

The region is the smallest convex region that includes the points:

A 2D convex hull mesh:

The region is the smallest convex region that includes the points:

A 3D convex hull mesh:

The region is the smallest convex region that includes the points:

Scope  (3)

Create a 1D convex hull mesh from a set of points:

Basic properties:

Convex hull meshes are bounded:

Convex hull meshes are full dimensional:

Find its area and centroid:

Test for point membership:

Find the nearest point and its distance:

Create a 2D convex hull mesh from a set of points:

Basic properties:

Convex hull meshes are bounded:

Convex hull meshes are full dimensional:

Find its area and centroid:

Test for point membership:

Find the nearest point and its distance:

Create a 3D convex hull mesh from a set of points:

Basic properties:

Convex hull meshes are bounded:

Convex hull meshes are full dimensional:

Find its volume and centroid:

Find its surface area:

Find the nearest point and its distance:

Options  (13)

MeshCellHighlight  (3)

MeshCellHighlight allows you to specify highlighting for parts of a ConvexHullMesh:

By making faces transparent, the internal structure of a 3D ConvexHullMesh can be seen:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

MeshCellLabel  (2)

MeshCellLabel can be used to label parts of a ConvexHullMesh:

Individual cells can be labeled using their cell index:

Or by the cell itself:

MeshCellMarker  (1)

MeshCellMarker can be used to assign values to parts of a ConvexHullMesh:

Use MeshCellLabel to show the markers:

MeshCellShapeFunction  (2)

MeshCellShapeFunction allows you to specify functions for parts of a ConvexHullMesh:

Individual cells can be drawn using their cell index:

Or by the cell itself:

MeshCellStyle  (3)

MeshCellStyle allows you to specify styling for parts of a ConvexHullMesh:

By making faces transparent, the internal structure of a 3D ConvexHullMesh can be seen:

Individual cells can be highlighted using their cell index:

Or by the cell itself:

PlotTheme  (2)

Use a theme with grid lines and a legend:

Use a theme to draw a wireframe:

Applications  (2)

The convex hull of a compound of five tetrahedra is a dodecahedron:

Compute the convex hull of a cow:

Visualize convex hull and cow:

Properties & Relations  (3)

ConvexHullMesh is effectively the BoundaryMesh of a DelaunayMesh:

In 3D:

Use DelaunayMesh to get a Delaunay triangulation of the interior of the convex hull:

Use TriangulateMesh to control the triangulation of the interior:

Possible Issues  (1)

ConvexHullMesh returns full–dimensional mesh regions only:

Use ConvexHullRegion to get the convex hull:

Wolfram Research (2014), ConvexHullMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvexHullMesh.html (updated 2020).

Text

Wolfram Research (2014), ConvexHullMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvexHullMesh.html (updated 2020).

CMS

Wolfram Language. 2014. "ConvexHullMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/ConvexHullMesh.html.

APA

Wolfram Language. (2014). ConvexHullMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvexHullMesh.html

BibTeX

@misc{reference.wolfram_2024_convexhullmesh, author="Wolfram Research", title="{ConvexHullMesh}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConvexHullMesh.html}", note=[Accessed: 23-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_convexhullmesh, organization={Wolfram Research}, title={ConvexHullMesh}, year={2020}, url={https://reference.wolfram.com/language/ref/ConvexHullMesh.html}, note=[Accessed: 23-November-2024 ]}