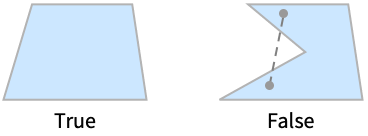
ConvexPolygonQ[poly]
gives True if the polygon poly is convex, and False otherwise.


ConvexPolygonQ
ConvexPolygonQ[poly]
gives True if the polygon poly is convex, and False otherwise.
Examples
open all close allBasic Examples (2)
Scope (7)
ConvexPolygonQ works on polygons:
Polygons with disconnected components:
ConvexPolygonQ works on polygons of geographic entities:
Polygons with GeoPosition:
Polygons with GeoPositionXYZ:
Polygons with GeoPositionENU:
ConvexPolygonQ works on polygons with GeoGridPosition:
Applications (4)
Generate random polygons for testing algorithms and verification of time complexity:
Time complexity for algorithms for convex polygons:
Test whether a polygon is concave:
Attempt to test whether a geometric region is convex:
Polygon classification using machine learning. Train a classifier function on polygon examples:
Properties & Relations (6)
The OuterPolygon of a convex polygon is convex:
Convex polygons do not have inner polygons:
A convex polygon has all interior vertex angles less than ![]() :
:
Use PolygonDecomposition to decompose a polygon into convex polygons:
Use RandomPolygon to generate a convex polygon:
Possible Issues (1)
For a nonconstant polygon, ConvexPolygonQ returns False:
Related Guides
-
▪
- Polygons
History
Text
Wolfram Research (2019), ConvexPolygonQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ConvexPolygonQ.html.
CMS
Wolfram Language. 2019. "ConvexPolygonQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ConvexPolygonQ.html.
APA
Wolfram Language. (2019). ConvexPolygonQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvexPolygonQ.html
BibTeX
@misc{reference.wolfram_2025_convexpolygonq, author="Wolfram Research", title="{ConvexPolygonQ}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/ConvexPolygonQ.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_convexpolygonq, organization={Wolfram Research}, title={ConvexPolygonQ}, year={2019}, url={https://reference.wolfram.com/language/ref/ConvexPolygonQ.html}, note=[Accessed: 25-January-2026]}