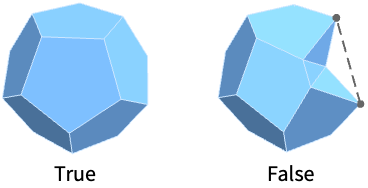
ConvexPolyhedronQ

ConvexPolyhedronQ[poly]

gives True if the polyhedron poly is convex, and False otherwise.

Details

A polyhedron is convex if no line segment between two points ever goes outside the polyhedron.

Examples

open allclose all

Basic Examples (2)

Test whether a polyhedron is convex:

ConvexPolyhedronQ gives False for non-convex polyhedrons:

Scope (3)

ConvexPolyhedronQ works on polyhedrons:

Polyhedron with holes:

Polyhedron with disconnected components:

Properties & Relations (3)

A convex polyhedron is simple:

The OuterPolyhedron of a convex polyhedron is convex:

Convex polyhedrons do not have holes:

The UniformPolyhedron is convex:

Possible Issues (1)

For nonconstant polyhedron, ConvexPolyhedronQ returns False:

Top

Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how