RandomPolyhedron[spec]
gives a pseudorandom polyhedron with the specified specification spec.
RandomPolyhedron[spec,k]
gives a list of k pseudorandom polyhedra.


RandomPolyhedron
RandomPolyhedron[spec]
gives a pseudorandom polyhedron with the specified specification spec.
RandomPolyhedron[spec,k]
gives a list of k pseudorandom polyhedra.
Details and Options

- RandomPolyhedron gives a Polyhedron drawn from a specific distribution.
- RandomPolyhedron is typically used in testing and verification of time complexity for algorithms.
- Possible specifications spec include:
-
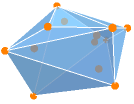
{"ConvexHull",dist,n} convex hull of n random points from the distribution dist - RandomPolyhedron[{"ConvexHull",n}] gives the convex hull of n random points from the uniform distribution UniformDistribution[3] over the unit square.
- RandomPolyhedron[spec,{k1,k2,…}] gives k1×k2×… arrays of pseudorandom polyhedra.
- RandomPolyhedron gives a different sequence of pseudorandom polyhedra whenever you run the Wolfram Language. By using SeedRandom, you can get a repeatable sequence.
- RandomPolyhedron has the same options as Polyhedron with the following additions: [List of all options]
-
DataRange Automatic the range of vertex points to generate WorkingPrecision MachinePrecision precision of vertex points - With the default setting DataRangeAutomatic, coordinates are chosen in the range 0 to 1.
-
DataRange Automatic the range of vertex points to generate VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures WorkingPrecision MachinePrecision precision of vertex points
List of all options
Examples
open all close allBasic Examples (2)
Scope (4)
Options (2)
DataRange (1)
DataRange allows you to specify the range of vertex points to generate:
Applications (3)
Basic Uses (2)
Properties & Relations (5)
Use SeedRandom to get repeatable random polyhedra:
Use BlockRandom to block one use of RandomPolyhedron from affecting others:
Use ConvexPolyhedronQ to check the property of a random polyhedron:
The OuterPolyhedron of a random polyhedron is simple:
Random polyhedra do not have voids:
Using PolyhedronDecomposition to decompose a polyhedron into tetrahedra:
Related Guides
History
Text
Wolfram Research (2019), RandomPolyhedron, Wolfram Language function, https://reference.wolfram.com/language/ref/RandomPolyhedron.html.
CMS
Wolfram Language. 2019. "RandomPolyhedron." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RandomPolyhedron.html.
APA
Wolfram Language. (2019). RandomPolyhedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RandomPolyhedron.html
BibTeX
@misc{reference.wolfram_2025_randompolyhedron, author="Wolfram Research", title="{RandomPolyhedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/RandomPolyhedron.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_randompolyhedron, organization={Wolfram Research}, title={RandomPolyhedron}, year={2019}, url={https://reference.wolfram.com/language/ref/RandomPolyhedron.html}, note=[Accessed: 06-January-2026]}