CoxIngersollRossProcess[μ,σ,θ,x0]
represents a Cox–Ingersoll–Ross process with long‐term mean μ, volatility σ, speed of adjustment θ, and initial condition x0.


CoxIngersollRossProcess
CoxIngersollRossProcess[μ,σ,θ,x0]
represents a Cox–Ingersoll–Ross process with long‐term mean μ, volatility σ, speed of adjustment θ, and initial condition x0.
Details
- CoxIngersollRossProcess is also known as the CIR process.
- CoxIngersollRossProcess is a continuous‐time and continuous‐state random process.
- The state
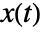 of the Cox–Ingersoll–Ross process satisfies an Ito differential equation
of the Cox–Ingersoll–Ross process satisfies an Ito differential equation 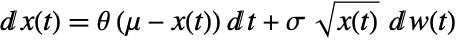 , where
, where 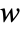 follows a standard WienerProcess[].
follows a standard WienerProcess[]. - CoxIngersollRossProcess allows x0 to be any positive real number, σ to be any nonzero real number, and θ and μ to be any nonzero real numbers of the same sign.
- CoxIngersollRossProcess can be used with such functions as Mean, PDF, Probability, and RandomFunction.
Examples
open all close allBasic Examples (3)
Scope (14)
Basic Uses (9)
Simulate an ensemble of random paths for a Cox–Ingersoll–Ross process:
Simulate with arbitrary precision:
Compare paths for different values of the drift parameter:
Compare paths for different values of the volatility parameter:
Compare paths for different values of the speed adjustment parameter:
Simulate a Cox–Ingersoll–Ross process with different starting points:
Process Slice Properties (5)
First-order probability density function for the slice distribution:
Multivariate slice distributions:
Compute the expectation of an expression:
Calculate the probability of an event:
CentralMoment and its generating function:
FactorialMoment and its generating function:
Cumulant and its generating function:
Properties & Relations (3)
A Cox–ingersoll–Ross process is not weakly stationary:
Conditional cumulative distribution function:
A Cox–ingersoll–Ross process is a special ItoProcess:
As well as StratonovichProcess:
Neat Examples (3)
Related Guides
History
Text
Wolfram Research (2012), CoxIngersollRossProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/CoxIngersollRossProcess.html.
CMS
Wolfram Language. 2012. "CoxIngersollRossProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoxIngersollRossProcess.html.
APA
Wolfram Language. (2012). CoxIngersollRossProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoxIngersollRossProcess.html
BibTeX
@misc{reference.wolfram_2025_coxingersollrossprocess, author="Wolfram Research", title="{CoxIngersollRossProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CoxIngersollRossProcess.html}", note=[Accessed: 06-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_coxingersollrossprocess, organization={Wolfram Research}, title={CoxIngersollRossProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/CoxIngersollRossProcess.html}, note=[Accessed: 06-January-2026]}