ItoProcess[{a,b},x,t]
represents an Ito process ![]() , where
, where ![]() .
.
ItoProcess[{a,b,c},x,t]
represents an Ito process ![]() , where
, where ![]() .
.
ItoProcess[…,{x,x0},{t,t0}]
uses initial condition ![]() .
.
ItoProcess[…,…,…,Σ]
uses a Wiener process ![]() , with covariance Σ.
, with covariance Σ.
ItoProcess[proc]
converts proc to a standard Ito process whenever possible.
ItoProcess[sdeqns,expr,x,t,wdproc]
represents an Ito process specified by a stochastic differential equation sdeqns, output expression expr, with state x and time t, driven by w following the process dproc.


ItoProcess
ItoProcess[{a,b},x,t]
represents an Ito process ![]() , where
, where ![]() .
.
ItoProcess[{a,b,c},x,t]
represents an Ito process ![]() , where
, where ![]() .
.
ItoProcess[…,{x,x0},{t,t0}]
uses initial condition ![]() .
.
ItoProcess[…,…,…,Σ]
uses a Wiener process ![]() , with covariance Σ.
, with covariance Σ.
ItoProcess[proc]
converts proc to a standard Ito process whenever possible.
ItoProcess[sdeqns,expr,x,t,wdproc]
represents an Ito process specified by a stochastic differential equation sdeqns, output expression expr, with state x and time t, driven by w following the process dproc.
Details and Options



- ItoProcess is also known as Ito diffusion or stochastic differential equation (SDE).
- ItoProcess is a continuous-time and continuous-state random process.
- If the drift a is an
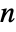 -dimensional vector and the diffusion b an
-dimensional vector and the diffusion b an 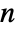 ×
×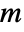 -dimensional matrix, the process is
-dimensional matrix, the process is 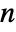 -dimensional and driven by an
-dimensional and driven by an 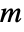 -dimensional WienerProcess.
-dimensional WienerProcess. - Common specifications for coefficients a and b include:
-
a scalar, b scalar 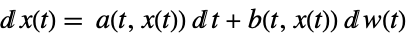
a scalar, b vector 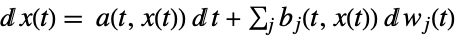
a vector, b vector 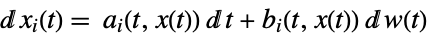
a vector, b matrix 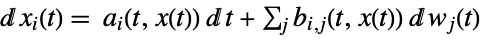
- A stochastic differential equation
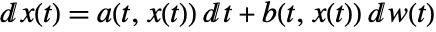 is sometimes written as an integral equation
is sometimes written as an integral equation 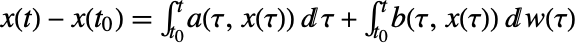 .
. - The default initial time t0 is taken to be zero, and the default initial state x0 is zero.
- The default covariance Σ is the identity matrix.
- For a general covariance Σ, ItoProcess canonicalizes the process by converting the diffusion matrix b to b.Σ1/2, with Σ1/2 the lower Cholesky factor of Σ when possible. »
- A standard Ito process has output
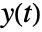 , consisting of a subset of differential states
, consisting of a subset of differential states 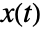 .
. - Processes proc that can be converted to standard ItoProcess form include OrnsteinUhlenbeckProcess, GeometricBrownianMotionProcess, StratonovichProcess, and ItoProcess.
- Converting an ItoProcess to standard form automatically makes use of Ito's lemma.
- The stochastic differential equations in sdeqns can be of the form
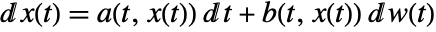 , where
, where 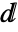 is \[DifferentialD], which can be input using
is \[DifferentialD], which can be input using  dd
dd . The differentials
. The differentials 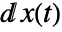 and
and 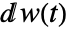 are taken to be Ito differentials.
are taken to be Ito differentials. - The output expression expr can be any expression involving x[t] and t.
- The driving process dproc can be any process that can be converted to a standard Ito process.
- Properties related to ItoProcess include:
-
"Drift" drift term "Diffusion" diffusion matrix "Output" output state "TimeVariable" time variable "TimeOrigin" origin of time variable "StateVariables" state variables "InitialState" initial state values "KolmogorovForwardEquation" Kolmogorov forward equation (Fokker-Planck equation) "KolmogorovBackwardEquation" Kolmogorov backward equation "Derivative" Ito derivative "FeynmanKacFormula" PDE obtained from Feynman-Kac formula - Method settings in RandomFunction specific to ItoProcess include: »
-
"EulerMaruyama" Euler–Maruyama (order 1/2, default) "KloedenPlatenSchurz" Kloeden–Platen–Schurz (order 3/2) "Milstein" Milstein (order 1) "StochasticRungeKutta" 3‐stage Rossler SRK scheme (order 1) "StochasticRungeKuttaScalarNoise" 3‐stage Rossler SRK scheme for scalar noise (order 3/2) - ItoProcess can be used with such functions as RandomFunction, CovarianceFunction, PDF, and Expectation.
Examples
open all close allBasic Examples (1)
Scope (19)
Basic Uses (10)
Define a Wiener process with drift ![]() and diffusion
and diffusion ![]() from the stochastic differential equation (SDE)
from the stochastic differential equation (SDE) ![]() :
:
Directly convert from the parametric process:
Use differential notation to define the same process:
Define a vector process ![]() with output
with output ![]() :
:
Define a vector process ![]() , where
, where ![]() :
:
Define a vector process ![]() where
where ![]() :
:
Define a process driven by two correlated Wiener processes:
The canonicalized process has diffusion matrix equal to ![]() , with
, with ![]() the diffusion matrix before canonicalization:
the diffusion matrix before canonicalization:
Define a scalar process ![]() corresponding to the SDE
corresponding to the SDE ![]() :
:
Define vector process ![]() and
and ![]() corresponding to the SDE
corresponding to the SDE ![]() and
and ![]() :
:
Define a process corresponding to the 2D correlated Wiener process:
Define vector process driven by correlated 2D Wiener process:
Simulate ItoProcess paths using different methods:
Simulation methods and their corresponding orders:
Specify the simulation method as an option in RandomFunction:
Process Properties Extraction (2)
Define an Ito process by its stochastic differential equation:
Available Ito process properties:
Drift and diffusion of the process:
Inactive is used here to avoid expanding the partial derivatives; use Activate to expand the expression:
Compute the Ito derivative of a function ![]() . The output is a list consisting of drift and diffusion terms:
. The output is a list consisting of drift and diffusion terms:
The property "FeynmanKacFormula" gives a PDE whose solution ![]() satisfies the conditional expectation
satisfies the conditional expectation ![]() and terminal condition
and terminal condition ![]() :
:
Additional arguments can be provided for the generalized situations. With an additional argument ![]() , the property "FeynmanKacFormula" gives a PDE whose solution satisfies the conditional expectation
, the property "FeynmanKacFormula" gives a PDE whose solution satisfies the conditional expectation ![]() and the same terminal condition:
and the same terminal condition:
With a third argument ![]() , the property "FeynmanKacFormula" gives a PDE whose solution satisfies the conditional expectation
, the property "FeynmanKacFormula" gives a PDE whose solution satisfies the conditional expectation ![]() and the same terminal condition:
and the same terminal condition:
Define Heston model with ItoProcess:
Special Ito Processes (5)
An Ito process corresponding to the WienerProcess:
An Ito process corresponding to the GeometricBrownianMotionProcess:
An Ito process corresponding to the BrownianBridgeProcess:
An Ito process corresponding to the OrnsteinUhlenbeckProcess:
An Ito process corresponding to the CoxIngersollRossProcess:
Process Slice Properties (2)
Define Jacobi diffusion process:
Compute low-order cumulants of time‐slice distribution:
Find the limit of infinite time horizon:
Compare with cumulants of the uniform distribution:
Define a vector process given by a system of linear SDEs:
Find the probability density function of the time‐slice distribution:
Applications (11)
Computing Properties (3)
Compute cross-covariance of the Ornstein–Uhlenbeck process ![]() and its underlying Wiener process
and its underlying Wiener process ![]() :
:
Compute moments of the process ![]() , where
, where ![]() is the standard Wiener process:
is the standard Wiener process:
Vector Ito process driven by scalar noise (1D oscillator driven by white noise):
Compute mean and variance functions:
Plot mean function and the standard deviation band, together with generated paths:
Martingales (3)
Determine values of ![]() and
and ![]() for which the process
for which the process ![]() is a martingale, where
is a martingale, where ![]() is the standard Wiener process:
is the standard Wiener process:
Zero drift coefficient of the standard form is a necessary condition for ![]() to be a martingale:
to be a martingale:
Scalar Ito process driven by vector Wiener process:
Define the same process via a stochastic equation:
Construct a scalar process driven by two Wiener processes:
By Lévy characterization, ![]() is a Brownian motion. The mean of the process is the same as the initial state:
is a Brownian motion. The mean of the process is the same as the initial state:
Modeling (2)
The dynamics of a free particle under the effect of thermal fluctuation can be modeled by the Langevin equation of motion, ![]() , where
, where ![]() is the standard WienerProcess and
is the standard WienerProcess and ![]() is the strength of the thermal noise. Here it is assumed that
is the strength of the thermal noise. Here it is assumed that ![]() can only depend on
can only depend on ![]() and focus on the equation of velocity. There are two common ways to integrate the equation of motion: Ito formulation and Stratonovich formulation. They can be defined via:
and focus on the equation of velocity. There are two common ways to integrate the equation of motion: Ito formulation and Stratonovich formulation. They can be defined via:
When ![]() is a constant, the two formulations are identical and lead to the same stationary distribution as
is a constant, the two formulations are identical and lead to the same stationary distribution as ![]() :
:
If ![]() is velocity dependent, then due to the nature of the WienerProcess,
is velocity dependent, then due to the nature of the WienerProcess, ![]() has nonzero quadratic variation and the two formulations lead to different results. Convert Stratonovich formulation to the equivalent Ito formulation:
has nonzero quadratic variation and the two formulations lead to different results. Convert Stratonovich formulation to the equivalent Ito formulation:
The drift under Stratonovich formulation is different from the drift under Ito formulation:
The Gompertz curve is typically used in the modeling of a growth process, such as tumor growth. By assuming Gaussian noise in the logarithm of the growth process, you can write the model as a stochastic differential equation:
Mean of the process is the usual Gompertz curve:
Slice distribution of the process at time ![]() obeys LogNormalDistribution:
obeys LogNormalDistribution:
Simulate the process with ![]() , and
, and ![]() from
from ![]() to
to ![]() :
:
Generate a thousand samples with the same conditions, then visualize the paths and slice data at ![]() :
:
Ito Process Representations (3)
Use ItoProcess to represent the standard WienerProcess:
![]() is a martingale. Use Ito lemma to compute the derivative of
is a martingale. Use Ito lemma to compute the derivative of ![]() :
:
Create a CoxIngersollRossProcess and represent it with ItoProcess:
Obtain Kolmogorov forward equation:
Solve the equation numerically in ![]() with a localized initial condition at
with a localized initial condition at ![]() and Dirichlet boundary conditions:
and Dirichlet boundary conditions:
Plot the solution of Kolmogorov forward equation at ![]() and compare it with the closed-form density function:
and compare it with the closed-form density function:
Visualize the dynamic of the solution with Animate:
Represent a GeometricBrownianMotionProcess with ItoProcess, where ![]() represents the risk-free interest rate and
represents the risk-free interest rate and ![]() is the volatility:
is the volatility:
Compute Ito differential for a discounted process ![]() :
:
The classical Black–Scholes equation can be obtained by equating the drift to 0 with some simplifications:
The equation can be also obtained directly from the Feynman–Kac formula:
Solve the Black–Scholes equation symbolically with DSolve:
Properties & Relations (2)
Convert StratonovichProcess to ItoProcess:
Transformed Wiener processes are related to ItoProcess:
Possible Issues (2)
ItoProcess does not support random initial conditions, so cannot be represented:
But it supports processes with fixed initial condition:
Initial time of the driven process needs to match with ItoProcess:
Text
Wolfram Research (2012), ItoProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/ItoProcess.html (updated 2016).
CMS
Wolfram Language. 2012. "ItoProcess." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ItoProcess.html.
APA
Wolfram Language. (2012). ItoProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ItoProcess.html
BibTeX
@misc{reference.wolfram_2025_itoprocess, author="Wolfram Research", title="{ItoProcess}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/ItoProcess.html}", note=[Accessed: 25-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_itoprocess, organization={Wolfram Research}, title={ItoProcess}, year={2016}, url={https://reference.wolfram.com/language/ref/ItoProcess.html}, note=[Accessed: 25-January-2026]}