OrnsteinUhlenbeckProcess[μ,σ,θ]
represents a stationary Ornstein–Uhlenbeck process with long-term mean μ, volatility ![]() , and mean reversion speed θ.
, and mean reversion speed θ.
OrnsteinUhlenbeckProcess[μ,σ,θ,x0]
represents an Ornstein–Uhlenbeck process with initial condition x0.


OrnsteinUhlenbeckProcess
OrnsteinUhlenbeckProcess[μ,σ,θ]
represents a stationary Ornstein–Uhlenbeck process with long-term mean μ, volatility ![]() , and mean reversion speed θ.
, and mean reversion speed θ.
OrnsteinUhlenbeckProcess[μ,σ,θ,x0]
represents an Ornstein–Uhlenbeck process with initial condition x0.
Details

- OrnsteinUhlenbeckProcess is a continuous-time and continuous-state random process.
- OrnsteinUhlenbeckProcess is also known as Vasicek model.
- The state
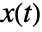 of an Ornstein–Uhlenbeck process satisfies an Ito differential equation
of an Ornstein–Uhlenbeck process satisfies an Ito differential equation 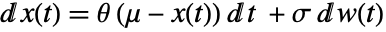 , where
, where 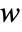 follows a standard WienerProcess[].
follows a standard WienerProcess[]. - The initial value for OrnsteinUhlenbeckProcess[μ,σ,θ] is random and follows NormalDistribution[μ,σ/
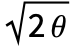 ].
]. - OrnsteinUhlenbeckProcess[μ,σ,θ] value at time t follows NormalDistribution[μ,σ/
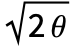 ].
]. - OrnsteinUhlenbeckProcess[μ,σ,θ,x0] value at time t follows NormalDistribution[ μ+(x0-μ)exp(-θ t),
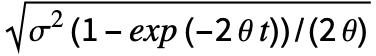 ].
]. - OrnsteinUhlenbeckProcess allows μ and x0 to be any real numbers and σ and θ to be any positive real numbers.
- OrnsteinUhlenbeckProcess can be used with such functions as Mean, PDF, Probability, and RandomFunction.
Examples
open all close allBasic Examples (3)
Scope (12)
Basic Uses (7)
Process Slice Properties (5)
Univariate SliceDistribution:
Probability density function does not depend on time:
Probability density function does depend on time:
Multivariate slice distribution:
Compute the expectation of an expression:
Calculate the probability of an event:
Skewness and kurtosis are constant:
CentralMoment and its generating function:
FactorialMoment has no closed form for symbolic order:
Cumulant and its generating function:
Generalizations & Extensions (1)
Properties & Relations (9)
OrnsteinUhlenbeckProcess starting at a random value is weakly stationary:
The process starting at a fixed value is not weakly stationary:
Power spectrum of a stationary Ornstein–Uhlenbeck process:
Ornstein–Uhlenbeck process has a well-defined StationaryDistribution:
Ornstein–Uhlenbeck process does not have independent increments:
Compare to the product of expectations:
Compare to the product of expectations:
Conditional cumulative distribution function:
An Ornstein–Uhlenbeck process with a fixed initial condition is a special ItoProcess:
As well as StratonovichProcess:
Ornstein–Uhlenbeck process is a solution of the stochastic differential equation ![]() :
:
Compare with the corresponding smooth solution:
Ornstein–Uhlenbeck with three arguments is mean ergodic:
The process is weakly stationary:
Calculate absolute correlation function:
Find value of the strip integral:
The process is mean ergodic only for μ=0:
Ornstein–Uhlenbeck process at integer times behaves as a first-order ARProcess:
Create moment equations to find parameters for an ARProcess:
Create an ARProcess:
Neat Examples (3)
Related Guides
History
Text
Wolfram Research (2012), OrnsteinUhlenbeckProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html.
CMS
Wolfram Language. 2012. "OrnsteinUhlenbeckProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html.
APA
Wolfram Language. (2012). OrnsteinUhlenbeckProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html
BibTeX
@misc{reference.wolfram_2025_ornsteinuhlenbeckprocess, author="Wolfram Research", title="{OrnsteinUhlenbeckProcess}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html}", note=[Accessed: 17-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ornsteinuhlenbeckprocess, organization={Wolfram Research}, title={OrnsteinUhlenbeckProcess}, year={2012}, url={https://reference.wolfram.com/language/ref/OrnsteinUhlenbeckProcess.html}, note=[Accessed: 17-January-2026]}