WOLFRAM

Wolfram Language & System Documentation Center

CoxModel[…]

represents the symbolic proportional hazards model obtained from CoxModelFit.

Details and Options
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Options  
ConfidenceLevel  
ConfidenceRange  
ConfidenceTransform  
See Also
Related Guides
History
Cite this Page

CoxModel

CoxModel[…]

represents the symbolic proportional hazards model obtained from CoxModelFit.

Details and Options

  • Properties of a Cox model are obtained from CoxModel[…]["property"].
  • CoxModel[…][{prop1,prop2,…}] gives several properties.
  • CoxModel[…][x0][t] gives the value of the best-fit function at a particular point t for covariate levels x0.
  • Normal gives the expression for the baseline survival function in a CoxModel.
  • CoxModel[…][prop,ann] gives the annotation ann associated with the property prop.
  • Possible properties available for a given type of fitted model are listed on the pages for functions such as CoxModelFit that generate the model.
  • CoxModel takes the following options:
  • ConfidenceLevel 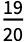confidence level to use for parameters and predictions
    ConfidenceRange Allrange for simultaneous confidence bands
    ConfidenceTransform "LogLog"confidence transform to use

Examples

open all close all

Basic Examples  (1)

Create a CoxModel from some right-censored data:

Extract a property from the model:

Evaluate the baseline survival function at 3:

Use normal to obtain the baseline survival function:

Obtain a list of available properties:

Scope  (5)

Extract a property from a CoxModel object:

The standard errors for the baseline survival function:

Obtain a list of properties:

Evaluate the baseline survival function at a point:

Map over several points:

Obtain an expression for the baseline survival function:

Annotate a property:

Options  (5)

ConfidenceLevel  (3)

The confidence level can be changed after fitting:

Plots of baseline survival with pointwise confidence bands:

Change the confidence level for parameter confidence intervals:

Use default confidence level:

The level can be changed after fitting:

Specify confidence level in summary tables:

Summarize the cumulative hazard function with 90% confidence limits:

ConfidenceRange  (1)

Set the confidence range for simultaneous intervals and bands:

The bands are only defined over the confidence range:

By default, the range is set to All:

Set the range to Full:

ConfidenceTransform  (1)

Apply transformations to confidence intervals and bands:

A collection of available transforms:

Bands for survival function at time 15:

Visualize the bands:

"LogLog" bands and intervals are used by default:

Wolfram Research (2012), CoxModel, Wolfram Language function, https://reference.wolfram.com/language/ref/CoxModel.html.

Text

Wolfram Research (2012), CoxModel, Wolfram Language function, https://reference.wolfram.com/language/ref/CoxModel.html.

CMS

Wolfram Language. 2012. "CoxModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoxModel.html.

APA

Wolfram Language. (2012). CoxModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoxModel.html

BibTeX

@misc{reference.wolfram_2025_coxmodel, author="Wolfram Research", title="{CoxModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CoxModel.html}", note=[Accessed: 16-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_coxmodel, organization={Wolfram Research}, title={CoxModel}, year={2012}, url={https://reference.wolfram.com/language/ref/CoxModel.html}, note=[Accessed: 16-August-2025]}