CoxModelFit[{e1,…,en}]
constructs a model of the baseline hazard ![]() for events times ei.
for events times ei.
CoxModelFit[{{{ξ11,…,ξ1p},…,{ξn1,…,ξnp}},{e1,…,en}},{f1,…,fm},{x1,…,xp}]
constructs a Cox model of the form ![]() , where the fi depend on the xk.
, where the fi depend on the xk.




CoxModelFit
CoxModelFit[{e1,…,en}]
constructs a model of the baseline hazard ![]() for events times ei.
for events times ei.
CoxModelFit[{{{ξ11,…,ξ1p},…,{ξn1,…,ξnp}},{e1,…,en}},{f1,…,fm},{x1,…,xp}]
constructs a Cox model of the form ![]() , where the fi depend on the xk.
, where the fi depend on the xk.
Details and Options







- CoxModelFit is used in survival, reliability, and duration analysis. It quantifies relative survival risk and estimates an underlying baseline hazard.
- CoxModelFit returns a symbolic CoxModel object to represent the proportional hazards model it constructs. The properties and diagnostics of the model can be obtained from model["property"].
- A list of available model properties can be obtained using model["Properties"].
- The form of events ei follows the form used in EventData.
- CoxModelFit produces a conditional hazard function
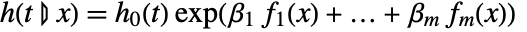 proportional to the baseline hazard function
proportional to the baseline hazard function 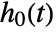 .
. - The model is semiparametric, with parameters
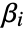 found by maximizing a partial likelihood. The baseline hazard
found by maximizing a partial likelihood. The baseline hazard 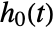 is estimated using nonparametric methods.
is estimated using nonparametric methods. - A null model that only estimates
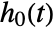 can be specified using CoxModelFit[e], which is equivalent to CoxModelFit[{ξ,e},{},{x1,…,xp}].
can be specified using CoxModelFit[e], which is equivalent to CoxModelFit[{ξ,e},{},{x1,…,xp}]. - Constant values specified in the basis functions fi are ignored in the fitting and absorbed in the estimation of the baseline hazard
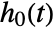 .
. - The following tables of properties pertain to the estimates, diagnostics, and testing of the parametric components
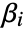 of the model. »
of the model. » - Properties related to data and the fitted function obtained using model["property"] include:
-
"BaselineList" list containing baseline covariate levels for each stratum "BasisFunctions" list of basis functions 
"BestFitParameters" parameter estimates 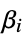
"Data" the matrix of covariate input data 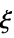
"EventData" the event input data 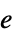
"RelativeRisk" relative risk 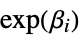 for the model parameters
for the model parameters"StrataModels" list containing submodels for each stratum "StrataSummary" list containing name and count pairings for each stratum - Properties that measure goodness of fit include:
-
"AIC" Akaike information criterion "BIC" Schwartz–Bayes information criterion "LogLikelihood" model log likelihood "MaxRSquared" maximum possible 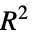 coefficient
coefficient"RSquared" pseudo coefficient of determination 
- Types of residuals and influence measures:
-
"BetaDifferences" DFBETAs measure of influence on parameter values "CoxSnellResiduals" Cox–Snell type residuals "DevianceResiduals" scaled Martingale residuals "MartingaleResiduals" estimate of the excess number of events over time "ScaledBetaDifferences" DFBETAs computed using the model standard deviation "SchoenfeldResiduals" Schoenfeld-type residuals "ScoreResiduals" score residuals - Properties and diagnostics for parameter estimates include:
-
"CovarianceMatrix" covariance estimate for model parameters "InformationMatrix" information matrix for model parameters "LikelihoodRatioStatistic" likelihood ratio of fitted model to the null model "ParameterConfidenceIntervals" confidence intervals about the parameter estimates "ParameterStandardErrors" standard errors of model parameters "ParameterTable" table of fitted parameter information "ParameterTableEntries" entries in the parameter table "RelativeRiskConfidenceIntervals" confidence intervals about relative risk estimates "RiskScores" risk scores for each observation "ScoreStatistic" score statistic comparing fitted and null models "TestTable" table of significance information for model parameters "TestTableEntries" entries from the test table "TestTableEntriesFunction" entries from table created with test table function "TestTableFunction" creates a test table under a specified null hypothesis "WaldStatistic" Wald statistic comparing fitted and null models - As in SurvivalModelFit, it is possible to obtain information about the nonparametric component of the model
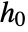 , including estimates of survival probabilities, survival confidence intervals, and moment estimates. »
, including estimates of survival probabilities, survival confidence intervals, and moment estimates. » - CoxModelFit has all of the properties available to SurvivalModelFit.
- Properties related to
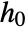 are specified as in SurvivalModelFit, but additionally require that the covariate level x0 be given as model["property"][x0].
are specified as in SurvivalModelFit, but additionally require that the covariate level x0 be given as model["property"][x0]. - Different functional forms of the hazard rate
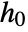 for covariate levels x0 can be obtained by specifying the form h in model[h][x0]. The following forms can be used.
for covariate levels x0 can be obtained by specifying the form h in model[h][x0]. The following forms can be used. -
"CDF" cumulative distribution function "CHF" cumulative hazard function "SF" survival function - The value of the fitted function h from CoxModelFit at a particular point t and covariate levels x0 can be found from model[h][x0][t]. model[h][][t] gives the form h of the baseline hazard h0[t].
- Specifying Normal[model] gives a pure function form of model["SF"][][t].
- CoxModelFit takes the following options:
-
ConfidenceLevel 95/100 level to use for intervals and bands ConfidenceRange All range for simultaneous confidence bands ConfidenceTransform "LogLog" confidence transform to use Method Automatic method to use for model fitting NominalVariables None variables considered as categorical StrataVariables None variables considered as strata WorkingPrecision Automatic precision used in internal computations - With ConfidenceLevel->p, probability-p confidence intervals and bands are computed for the various functional forms and parameter estimates.
- ConfidenceRange->{tmin,tmax} gives probability-p simultaneous confidence intervals and bands for the fitted function between tmin and tmax.
- Possible settings for ConfidenceTransform include "Linear", "LogLog", "ArcSinSqrt", "Log", "Logit", or a pure function g.
- The setting Method->m specifies the method for handling ties. Possible settings include the following.
-
"Breslow" use Breslow's partial likelihood "Efron" use Efron's partial likelihood "Exact" use the exact marginal likelihood - By default, the "Breslow" method is used for handling ties.
- Additional method settings can be found in the options section of examples. »
Examples
open all close allBasic Examples (1)
Scope (26)
Basic Uses (8)
Estimate and test parameters in a Cox proportional hazards model:
The parameter estimates for ![]() and
and ![]() both differ significantly from zero at the 5% level:
both differ significantly from zero at the 5% level:
Compare the fitted model to the null model, containing no covariates:
Form 95% confidence intervals about relative risk and parameter estimates:
Find survival probabilities and plot model estimates:
Compare survival for different levels of ![]() with
with ![]() fixed at 25 with the baseline survival:
fixed at 25 with the baseline survival:
Compute the median survival time for both levels of ![]() with
with ![]() fixed at 25:
fixed at 25:
The probability that an individual with levels ![]() and
and ![]() will survive beyond 20:
will survive beyond 20:
A 95% confidence interval for the same probability:
The number of observations in each stratum:
Plot different forms of the hazard for levels ![]() and
and ![]() :
:
Fit a model with categorical predictor variables:
Plots of the estimated CDFs for each level in the data:
Add interaction terms to the model:
No significant interaction is detected in the model:
Nominal and strata variables can be used in interaction terms:
Test model parameters against specific null hypotheses:
Test ![]() with the second parameter free:
with the second parameter free:
Use a contrast matrix to test a linear combination of the parameters:
Test the following null hypothesis:
Specifying only a contrast matrix tests a hypothesis of the following form:
Model Specification (4)
Create a model with no covariates ![]() (null model):
(null model):
The model is simply an estimate of the baseline survival:
Basis functions specify which of the available variables should be included in the model:
Parameter estimates corresponding to each of the four covariates:
Not all variables must be used in the basis functions:
Basis functions also control the functional form of model terms:
Parameter estimates for the terms in the model:
Use EventData to specify right-censored or left-truncated response times:
Parameter Estimates and Model Diagnostics (6)
Obtain parameter estimates and parameter confidence intervals:
The model parameters ![]() and relative risk estimates
and relative risk estimates ![]() :
:
Confidence intervals about the parameter estimates:
Entries from the parameter table:
Obtain a variety of model residuals:
Martingale, Cox–Snell, and deviance residuals:
Score and Schoenfeld residuals:
Compute a selection of goodness-of-fit measures:
Perform global hypothesis tests:
Survival Estimates and Confidence Measures (8)
Compute estimates of the SurvivalFunction, CDF, or cumulative hazard function:
The estimated SurvivalFunction for covariate levels ![]() and
and ![]() :
:
The estimated baseline SurvivalFunction, CDF, and cumulative hazard at time ![]() :
:
Tabulate a summary of the estimated SurvivalFunction:
A survival summary for covariate levels ![]() and
and ![]() :
:
Properties of distribution function estimates default to "SF":
Tabulate the cumulative hazard function:
Compute pointwise confidence bands and intervals:
A set of pointwise survival confidence intervals for covariate levels ![]() and
and ![]() :
:
These are "PointwiseBands" evaluated at the model "EstimationPoints":
Estimate simultaneous confidence bands and intervals:
A set of Hall–Wellner simultaneous confidence intervals for covariate levels ![]() and
and ![]() :
:
These are "HallWellnerBands" evaluated at the model "EstimationPoints":
Alternatively, use "EqualPrecisionIntervals" to measure simultaneous confidence:
Plot survival estimates and confidence bands:
Plots of baseline survival and cumulative hazard with 95% pointwise confidence bands:
The same plots for covariate levels ![]() and
and ![]() :
:
Estimate median survival times:
The median survival time for covariate levels ![]() and
and ![]() and at the baseline:
and at the baseline:
The survival function does not reach zero due to right censoring; the mean is not well defined:
Adding a model for the remaining probability allows the mean to be estimated:
Options (13)
ConfidenceLevel (3)
Change the confidence level for parameter confidence intervals:
The level can be changed after fitting:
Plot survival estimates with 90% confidence bands:
Plots of baseline survival with 90% pointwise confidence bands:
The level can be changed after fitting:
The setting for ConfidenceLevel is also used in summary tables:
Summarize the cumulative hazard function with 90% confidence limits:
ConfidenceRange (1)
ConfidenceTransform (3)
Apply transformations to confidence intervals and bands:
A collection of available transforms:
"LogLog" bands and intervals are used by default:
Transformations can ensure that intervals and bands are appropriately bounded:
Notice that linear confidence limits may exceed 1. or be less than zero:
Using a "LogLog" transform corrects this issue:
Method (3)
Select the method used for handling tied event times:
The default method maximizes Breslow's partial likelihood:
When the proportion of ties is high, the estimates may differ considerably:
In the absence of tied event times, all of the methods are equivalent:
Choose an estimator for the baseline hazard:
By default, the baseline hazard estimator is matched to the tie method:
The estimators generally agree closely:
Any combination of tie and baseline method can be used:
If the last observation is censored, the survival will be Indeterminate beyond that point:
NominalVariables (1)
StrataVariables (1)
Applications (5)
Ear Mite Treatment (1)
A group of 16 dogs and 9 cats was selected to test a new treatment for ear mites. Each animal was randomly assigned to be treated with an older medication or the new drug. Determine whether the new treatment extends the time in weeks to ear mite reinfection:
Fit a proportional hazards model stratified on species:
The new treatment seems to significantly extend the time to ear mite reinfection:
Assess the fit using a Cox–Snell residual plot:
The plot suggests that the model is a reasonable fit to the data:
Larynx Cancer (3)
A group of 90 male patients diagnosed with cancer of the larynx was observed. Each patient was classified as having one of four stages of cancer with 1 being least severe and 4 most severe. Of interest is whether the stage of cancer is significantly linked to survival:
The table gives the relative risk of dying for each stage compared to stage 1:
The risk of dying for stage 2 patients is not different from stage 1 at the 5% level:
Find an estimate of the relative risk of death for stage 4 larynx cancer patients compared to those with stage 2 larynx cancer:
Parameter estimates for stage 2 and stage 4 larynx cancer:
Use the parameter covariance matrix to compute the standard error of the estimate:
At the 5% level, the risk of death is higher for stage 4 patients compared to stage 2 patients:
Visually compare the survival of 50-year-old patients in each stage:
Under a null hypothesis of no trend, test whether increasing the stage of larynx cancer increases the risk of dying:
Fit a Cox model stratified on stage:
LogRankTest can be used to perform a test for trend, given ordered strata:
The test statistic for trend based on the 4 levels of stage:
Reject the null hypothesis of nonpositive trend. Death rate appears to increase with stage:
Acute Leukemia (1)
A sample of 101 patients with advanced acute myelogenous leukemia was recorded. Fifty-one of these patients had received an autologous bone marrow transplant and 50 patients had an allogeneic bone marrow transplant. Of interest is whether a proportional hazards model would be valid for this data:
Fit a model stratified on transplant type:
The log cumulative hazards cross, indicating non-proportional hazards:
Properties & Relations (4)
Relative risk is ![]() of the parameter estimates
of the parameter estimates ![]() :
:
A unit increase in ![]() more than triples the risk of failure:
more than triples the risk of failure:
Relative risk can be more difficult to interpret when the parameter estimates are negative:
Compute absolute relative risk instead:
In this case the same result can be found by reversing the coding of ![]() :
:
CoxModelFit is a generalization of SurvivalModelFit:
Use LogRankTest to compare the hazard rates of groups:
A significant difference in hazard rates for the two groups is detected at the 5% level:
History
Text
Wolfram Research (2012), CoxModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/CoxModelFit.html.
CMS
Wolfram Language. 2012. "CoxModelFit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CoxModelFit.html.
APA
Wolfram Language. (2012). CoxModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CoxModelFit.html
BibTeX
@misc{reference.wolfram_2025_coxmodelfit, author="Wolfram Research", title="{CoxModelFit}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CoxModelFit.html}", note=[Accessed: 20-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_coxmodelfit, organization={Wolfram Research}, title={CoxModelFit}, year={2012}, url={https://reference.wolfram.com/language/ref/CoxModelFit.html}, note=[Accessed: 20-February-2026]}