LogRankTest[{data1,data2,…}]
tests for equal hazard rates among the datai using a log-rank type test.
LogRankTest[{data1,data2,…},wspec]
performs a weighted log-rank test with weights wspec.
LogRankTest[{data1,…},wspec,"property"]
returns the value of "property".


LogRankTest
LogRankTest[{data1,data2,…}]
tests for equal hazard rates among the datai using a log-rank type test.
LogRankTest[{data1,data2,…},wspec]
performs a weighted log-rank test with weights wspec.
LogRankTest[{data1,…},wspec,"property"]
returns the value of "property".
Details and Options



- LogRankTest performs a hypothesis test on the datai with null hypothesis
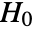 that the true hazard rates of the populations are equal
that the true hazard rates of the populations are equal 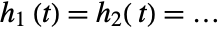 for all
for all 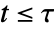 and alternative hypothesis
and alternative hypothesis 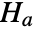 that at least one
that at least one 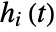 is different for some value of
is different for some value of 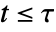 .
. - The number
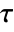 is generally taken to be the largest event time in the datai.
is generally taken to be the largest event time in the datai. - By default, a probability value or
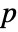 -value is returned.
-value is returned. - A small
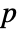 -value suggests that it is unlikely that
-value suggests that it is unlikely that 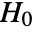 is true.
is true. - The datai must be univariate {x1,x2,…}.
- The datai can be a SparseArray or EventData object.
- LogRankTest is effectively based on
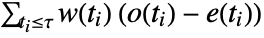 where
where 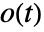 ,
, 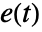 , and
, and 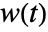 are the observed number of events, the expected number of events based on the pooled sample, and some weights, respectively.
are the observed number of events, the expected number of events based on the pooled sample, and some weights, respectively. - For named weight methods, the weight at time
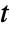 ,
, 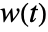 , is generally based on the number at risk
, is generally based on the number at risk 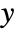 , the number of events
, the number of events 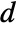 , the product limit estimator
, the product limit estimator 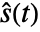 of the pooled sample, or a similar estimator
of the pooled sample, or a similar estimator 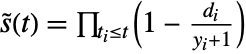 of the pooled sample.
of the pooled sample. - The following weight specifications wspec can be given:
-
ρ Fleming–Harrington weights with 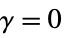
{ρ,γ} fully specified Fleming–Harrington weights "name" use a named weight method - The values of ρ and γ can be any non-negative numbers.
- Specifying ρ and γ yields Fleming–Harrington weights of the form
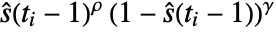 .
. - Possible named weight specifications include:
-
"AndersenPeto" 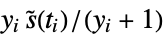
"Equal" 
"Gehan" 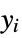
"Peto" 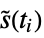
"TaroneWare" 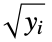
- For interval-censored data, the Zhao–Zhao–Sun–Kim generalized log-rank test is used.
- LogRankTest[{data1,…},wspec,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- LogRankTest[{data1,…},wspec,"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"DegreesOfFreedom" the degrees of freedom used in a test "EventTimes" list of time points used in the test "EventWeights" a list of weights used at each event time "PValue" list of 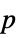 -values
-values"PValueTable" formatted table of 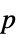 -values
-values"ShortTestConclusion" a short description of the conclusion of a test "TestConclusion" a description of the conclusion of a test "TestData" list of pairs of test statistics and 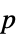 -values
-values"TestDataTable" formatted table of 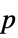 -values and test statistics
-values and test statistics"TestStatistic" list of test statistics "TestStatisticTable" formatted table of test statistics - The following options can be given:
-
Method Automatic the method to use for computing 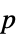 -values
-valuesSignificanceLevel 0.05 cutoff for diagnostics and reporting
Examples
open all close allBasic Examples (4)
Compare hazard rates using some sample data:
Create a HypothesisTestData object for repeated property extraction:
A significant difference is detected at the 5% level:
Perform a weighted log-rank test:
Use Fleming–Harrington weights:
Test for equal hazard rates with many samples:
Scope (11)
Testing (7)
Obtain the ![]() -value from a log-rank test:
-value from a log-rank test:
Simultaneously test a large number of groups:
Compute the ![]() -value for weighted log-rank tests:
-value for weighted log-rank tests:
Manually set Fleming–Harrington type weights:
Fleming–Harrington weights with ![]() and
and ![]() :
:
Use fully specified Fleming–Harrington type weights:
Fleming–Harrington weights with ![]() and
and ![]() :
:
Extract some properties from a HypothesisTestData object:
The ![]() -value and test statistic:
-value and test statistic:
Options (4)
Method (3)
By default, the asymptotic ![]() distribution of the test statistic is used to compute
distribution of the test statistic is used to compute ![]() -values:
-values:
Random permutation-based tests may give better results with small samples:
Specify the number of random permutations to perform:
Specify 250 random permutations:
Properties & Relations (7)
By default, the test statistic is assumed to follow a ChiSquareDistribution under ![]() :
:
Weighting schemes allow for particular time points to be emphasized:
Named schemes tend to place more weight on early events:
Fleming–Harrington parameters allow fine control over weighting:
MannWhitneyTest can be used in the absence of censoring with two samples:
The tests are asymptotically equivalent:
The Kruskal–Wallis test can be used in the absence of censoring with more than two samples:
The tests are asymptotically equivalent:
Use SurvivalModelFit to estimate survival probabilities:
Create a 95% confidence interval about the survival probability at 30:
Use CoxModelFit to estimate survival probabilities in the presence of covariates:
Visualize survival estimate at covariate levels ![]() and
and ![]() :
:
The log rank test recognizes the path structure of a TemporalData:
Related Guides
History
Text
Wolfram Research (2012), LogRankTest, Wolfram Language function, https://reference.wolfram.com/language/ref/LogRankTest.html.
CMS
Wolfram Language. 2012. "LogRankTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LogRankTest.html.
APA
Wolfram Language. (2012). LogRankTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogRankTest.html
BibTeX
@misc{reference.wolfram_2025_logranktest, author="Wolfram Research", title="{LogRankTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/LogRankTest.html}", note=[Accessed: 23-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_logranktest, organization={Wolfram Research}, title={LogRankTest}, year={2012}, url={https://reference.wolfram.com/language/ref/LogRankTest.html}, note=[Accessed: 23-February-2026]}