VarianceTest

VarianceTest[data]

tests whether the variance of the data is one.

VarianceTest[{data1,data2}]

tests whether the variances of data1 and data2 are equal.

VarianceTest[dspec,σ02]

tests a dispersion measure against σ02.

VarianceTest[dspec,σ02,"property"]

returns the value of "property".

Details and Options

  • VarianceTest tests the null hypothesis 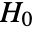against the alternative hypothesis :
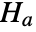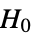
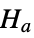
  • data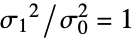
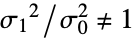
    {data1,data2}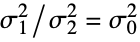
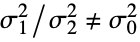
  • where σi2 is the population variance for datai.
  • By default, a probability value or 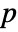-value is returned.
  • A small 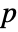-value suggests that it is unlikely that 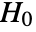is true.
  • The data in dspec must be univariate {x1,x2,…}.
  • The argument 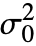can be any positive real number.
  • VarianceTest[dspec,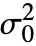] will choose the most powerful test that applies to dspec.
  • VarianceTest[dspec,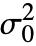,All] will choose all tests that apply to dspec.
  • VarianceTest[dspec,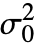,"test"] reports the 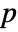-value according to "test".
  • Most tests require normally distributed data. If a test is less sensitive to a normality assumption, it is called robust. Some tests assume that data is symmetric around its medians.
  • The following tests can be used:
  • "BrownForsythe"robustrobust Levene test
    "Conover"symmetrybased on squared ranks of data
    "FisherRatio"normalitybased on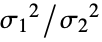
    "Levene"robust,symmetrycompare individual and group variances
    "SiegelTukey"symmetrybased on ranks of pooled data
  • VarianceTest[data,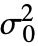,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • VarianceTest[data,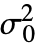,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "AllTests"list of all applicable tests
    "AutomaticTest"test chosen if Automatic is used
    "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"list of 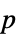-values
    "PValueTable"formatted table of 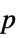-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 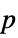-values
    "TestDataTable"formatted table of 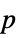-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • The following options can be given:
  • AlternativeHypothesis "Unequal"the inequality for the alternative hypothesis
    SignificanceLevel 0.05cutoff for diagnostics and reporting
    VerifyTestAssumptions Automaticset which diagnostic tests to run
  • For tests of variance, a cutoff 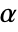is chosen such that 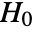is rejected only if 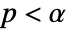. The value of 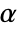used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 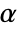is also used in diagnostic tests of assumptions, including tests for normality and symmetry. By default, 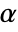is set to 0.05.
  • Named settings for VerifyTestAssumptions in VarianceTest include:
  • "Normality"verify that all data is normally distributed
    "Symmetry"verify symmetry about a common median

Examples

open allclose all

Basic Examples  (3)

Test variances from two populations for equality:

Create a HypothesisTestData object for further property extraction:

The full test table:

Compare the variance of a population to a particular value:

Test the ratio of the variances of two populations against a particular value:

Perform the test with alternative hypothesis :

Scope  (15)

Testing  (11)

Test whether the variance of a population is one:

The -values are typically large under :

The -values are typically small when is false:

Compare the variance of a population to a particular value:

Compare the variance of a quantity data to a particular value:

Compare the variances of two populations:

The -values are typically large when the variances are equal:

The -values are typically small when the variances are not equal:

Test whether the ratio of the variances of two populations is a particular value:

The following forms are equivalent:

The order of the datasets should be considered when determining :

Using Automatic applies the generally most powerful appropriate test:

The property "AutomaticTest" can be used to determine which test was chosen:

Perform a particular test for equal variance:

Any number of tests can be performed simultaneously:

Perform all tests appropriate to the data simultaneously:

Use the property "AllTests" to identify which tests were used:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value and test statistic from a Levene test:

Extract any number of properties simultaneously:

The -value and test statistic from the Brown–Forsythe test:

Reporting  (4)

Tabulate the results from a selection of tests:

A full table of all appropriate test results:

A table of selected test results:

Retrieve the entries from a test table for customized reporting:

The -values are above 0.05, so there is not enough evidence to reject normality at that level:

Tabulate -values for a test or group of tests:

The -value from the table:

A table of -values from all appropriate tests:

A table of -values from a subset of tests:

Report the test statistic from a test or group of tests:

The test statistic from the table:

A table of test statistics from all appropriate tests:

Options  (10)

AlternativeHypothesis  (3)

A two-sided test is performed by default:

Test versus :

Perform a two-sided test or a one-sided alternative:

Test versus :

Test versus :

Test versus :

Perform tests with one-sided alternatives when a null value is given:

Test versus :

Test versus :

SignificanceLevel  (3)

Set the significance level for diagnostic tests:

By default, 0.05 is used:

Setting the significance level may alter which test is automatically chosen:

A rank-based test would have been chosen by default:

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

VerifyTestAssumptions  (4)

Diagnostics can be controlled as a group using All or None:

Verify all assumptions:

Check no assumptions:

Diagnostics can be controlled independently:

Assume normality but check for symmetry:

Only check for normality:

Test assumption values can be explicitly set:

It is often useful to bypass diagnostic tests for simulation purposes:

The assumptions of the test hold by design, so a great deal of time can be saved:

The results are identical:

Applications  (2)

Test whether the variances of some populations are equivalent:

The first two populations have similar variances:

The third population differs in variance from the first:

An object with a length of 2.15 cm was measured with the same ruler by 25 grade-school students in two different classes:

The second group is superior in their precision:

Compare the accuracy of the groups using squared error:

The first group is significantly more accurate:

Properties & Relations  (7)

The -value suggests the expected proportion of false positives (Type I errors):

Setting the size of a test to 0.05 results in an erroneous rejection of about 5% of the time:

The power of each test is the probability of rejecting when it is false:

The power of the tests at six different levels. The Siegel–Tukey has the lowest power:

The power of the tests is proportional to the sample size:

The power of the tests is lower than in the previous example:

A two-sided -value is twice the smaller of the two one-sided -values:

The Brown–Forsythe and Levene tests are equivalent to the Fisher ratio test for a single sample:

The variance test works with the values only when the input is a TimeSeries:

The variance test works with all the values together when the input is a TemporalData:

Test all the values only:

Test whether the variances of the two paths are equal:

Possible Issues  (2)

The Conover and Siegel–Tukey tests are not defined for a single sample:

Some tests assume the data is normally distributed:

Conover's test and the Siegel–Tukey test do not assume normality:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), VarianceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceTest.html.

Text

Wolfram Research (2010), VarianceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceTest.html.

CMS

Wolfram Language. 2010. "VarianceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceTest.html.

APA

Wolfram Language. (2010). VarianceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceTest.html

BibTeX

@misc{reference.wolfram_2025_variancetest, author="Wolfram Research", title="{VarianceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceTest.html}", note=[Accessed: 05-July-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_variancetest, organization={Wolfram Research}, title={VarianceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/VarianceTest.html}, note=[Accessed: 05-July-2025 ]}