VarianceEquivalenceTest

VarianceEquivalenceTest[{data1,data2,…}]

tests whether the variances of the datai are equal.

VarianceEquivalenceTest[{data1,…},"property"]

returns the value of "property".

Details and Options

  • VarianceEquivalenceTest performs a hypothesis test on the datai with null hypothesis 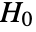that the true population variances are identical to 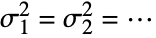, and alternative hypothesis 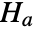that at least one is different.
  • By default, a probability value or 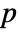-value is returned.
  • A small 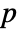-value suggests that it is unlikely that .
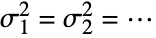  • The datai must be univariate {x1,x2,…}.
  • VarianceEquivalenceTest[{data1,…}] will choose the most powerful test that applies to the data.
  • VarianceEquivalenceTest[{data1,…},All] will choose all tests that apply to the data.
  • VarianceEquivalenceTest[{data1,…},"test"] reports the 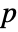-value according to "test".
  • Most tests require normally distributed datai. If a test is less sensitive to a normality assumption, it is called robust. Some tests assume that datai is symmetric around its medians.
  • The following tests can be used:
  • "Bartlett"normalitymodified likelihood ratio test
    "BrownForsythe"robustrobust Levene test
    "Conover"symmetryConover's squared ranks test
    "FisherRatio"normalitybased on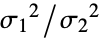
    "Levene"robust,symmetrycompares individual and group variances
  • VarianceEquivalenceTest[{data1,…},"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • VarianceEquivalenceTest[{data1,…},"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "AllTests"list of all applicable tests
    "AutomaticTest"test chosen if Automatic is used
    "DegreesOfFreedom"the degrees of freedom used in a test
    "PValue"list of 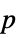-values
    "PValueTable"formatted table of 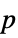-values
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"list of pairs of test statistics and 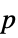-values
    "TestDataTable"formatted table of 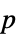-values and test statistics
    "TestStatistic"list of test statistics
    "TestStatisticTable"formatted table of test statistics
  • The following options can be given:
  • SignificanceLevel 0.05cutoff for diagnostics and reporting
    VerifyTestAssumptions Automaticset which diagnostic tests to run
  • For tests of variance, a cutoff 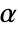is chosen such that 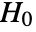is rejected only if 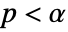. The value of 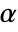used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 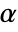is also used in diagnostic tests of assumptions, including tests for normality and symmetry. By default, 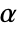is set to 0.05.
  • Named settings for VerifyTestAssumptions in VarianceEquivalenceTest include:
  • "Normality"verify that all data is normally distributed
    "Symmetry"verify that all data is symmetric

Examples

open allclose all

Basic Examples  (2)

Test variances from two datasets for equivalence:

Create a HypothesisTestData object for further property extraction:

The full test table:

Compare the variances of multiple datasets simultaneously:

The variances of the datasets:

Scope  (12)

Testing  (8)

Compare the variances of two datasets:

The -values are typically large when the variances are equal:

The -values are typically small when the variances are not equal:

Using Automatic applies the generally most powerful appropriate test:

The property "AutomaticTest" can be used to determine which test was chosen:

Compare the variances of many datasets simultaneously:

Compare the distributions of the datasets visually using SmoothHistogram:

Perform a particular test for equal variance:

Any number of tests can be performed simultaneously:

Perform all tests, appropriate to the data, simultaneously:

Use the property "AllTests" to identify which tests were used:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value and test statistic from a Levene test:

Extract any number of properties simultaneously:

The -value and test statistic from a Brown–Forsythe test:

Reporting  (4)

Tabulate the results from a selection of tests:

A full table of all appropriate test results:

A table of selected test results:

Retrieve the entries from a test table for customized reporting:

The -values are above 0.05, so there is not enough evidence to reject normality at that level:

Tabulate -values for a test or group of tests:

The -value from the table:

A table of -values from all appropriate tests:

A table of -values from a subset of tests:

Report the test statistic from a test or group of tests:

The test statistic from the table:

A table of test statistics from all appropriate tests:

Options  (6)

SignificanceLevel  (3)

Set the significance level for diagnostic tests:

The default level is 0.05:

Setting the significance level may alter which test is automatically chosen:

A rank-based test would have been chosen by default:

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

VerifyTestAssumptions  (3)

Diagnostics can be controlled as a group using All or None:

Verify all assumptions:

Check no assumptions:

Diagnostics can be controlled independently:

Assume normality but check for symmetry:

Only check for normality:

Test assumption values can be explicitly set:

The Conover test was previously chosen because the data is not normally distributed:

Applications  (2)

Test whether a group of populations shares a common variance:

The first group of datasets was drawn from populations with very different variances:

Populations represented by the second group all have similar variances:

LocationEquivalenceTest can be used to compare the means of several datasets simultaneously but requires that the datasets have common variance:

Use VarianceEquivalenceTest to determine if the variances are equivalent:

LocationEquivalenceTest can be used to compare the means:

Properties & Relations  (5)

The Brown–Forsythe and Levene tests are equivalent but use different standardizing functions:

The Levene test uses Mean to standardize the data:

The Brown–Forsythe test typically uses Median:

For heavy-tailed data, the 10% TrimmedMean is used instead:

For datasets and total observations, the Brown–Forsythe and Levene test statistics both follow FRatioDistribution[k-1,n-k] under :

Bartlett's test statistic:

Under , the test statistic follows ChiSquareDistribution[k-1]:

The variance equivalence test ignores the time stamps when the input is a TimeSeries:

The variance equivalence test recognizes the path structure of a TemporalData:

Use the values directly:

Possible Issues  (2)

The Fisher ratio test requires two datasets:

Use any of the other tests instead:

Conover's test is the only test that does not assume the data is normally distributed:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), VarianceEquivalenceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

Text

Wolfram Research (2010), VarianceEquivalenceTest, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

CMS

Wolfram Language. 2010. "VarianceEquivalenceTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html.

APA

Wolfram Language. (2010). VarianceEquivalenceTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html

BibTeX

@misc{reference.wolfram_2024_varianceequivalencetest, author="Wolfram Research", title="{VarianceEquivalenceTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html}", note=[Accessed: 22-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_varianceequivalencetest, organization={Wolfram Research}, title={VarianceEquivalenceTest}, year={2010}, url={https://reference.wolfram.com/language/ref/VarianceEquivalenceTest.html}, note=[Accessed: 22-December-2024 ]}