SmoothHistogram[{x1,x2,…}]
plots a smooth kernel histogram for the PDF of the values xi.
SmoothHistogram[{x1,x2,…},espec]
plots a smooth kernel histogram with estimator specification espec.
SmoothHistogram[{x1,x2,…},espec,dfun]
plots the distribution function dfun.
SmoothHistogram[{data1,data2,…},…]
plots smooth kernel histograms for multiple datasets datai.




SmoothHistogram
SmoothHistogram[{x1,x2,…}]
plots a smooth kernel histogram for the PDF of the values xi.
SmoothHistogram[{x1,x2,…},espec]
plots a smooth kernel histogram with estimator specification espec.
SmoothHistogram[{x1,x2,…},espec,dfun]
plots the distribution function dfun.
SmoothHistogram[{data1,data2,…},…]
plots smooth kernel histograms for multiple datasets datai.
Details and Options





- SmoothHistogram is also known as nonparametric kernel density estimator or kernel estimator.
- SmoothHistogram plots
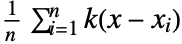 for a smoothing kernel
for a smoothing kernel 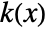 as an estimate of the PDF.
as an estimate of the PDF. - Data for SmoothHistogram can be given in the following forms:
-
{e1,e2,…} list of elements with or without wrappers <|k1y1,k2y2,…|> association of keys and lengths TimeSeries[…],EventSeries[…],TemporalData[…] time series, event series, and temporal data WeightedData[…],EventData[…] augmented datasets w[{e1,e2,…},…] wrapper applied to a whole dataset w[{data1,data1,…},…] wrapper applied to all datasets - SmoothHistogram[Tabular[…]cspec] extracts and plots values from the tabular object using the column specification cspec.
- The following forms of column specifications cspec are allowed for plotting tabular data:
-
colx create a smooth histogram for the values in column colx {colx1,colx2,…} create smooth histograms for columns colx1, colx2, … - The estimator specification espec can be of the form bw or {bw,kernel}.
- The specifications for bandwidth bw and kernel are the same as for SmoothKernelDistribution.
- Possible distribution functions dfun include:
-
"PDF" probability density function "Intensity" count density function "CDF" cumulative distribution function "SF" survival function "HF" hazard function "CHF" cumulative hazard function - The form w[data] provides a wrapper w to be applied to the resulting graphics primitives.
- The following wrappers can be used:
-
Annotation[e,label] provide an annotation Button[e,action] define an action to execute when the element is clicked EventHandler[e,…] define a general event handler for the element Highlighted[e,effect] dynamically highlight e with an effect Highlighted[e,Placed[effect,pos]] statically highlight e with an effect at position pos Hyperlink[e,uri] make the element act as a hyperlink PopupWindow[e,cont] attach a popup window to the element StatusArea[e,label] display in the status area when the element is moused over Style[e,opts] show the element using the specified styles Tooltip[e,label] attach an arbitrary tooltip to the element - SmoothHistogram has the same options as Graphics with the following additions and changes: [List of all options]
-
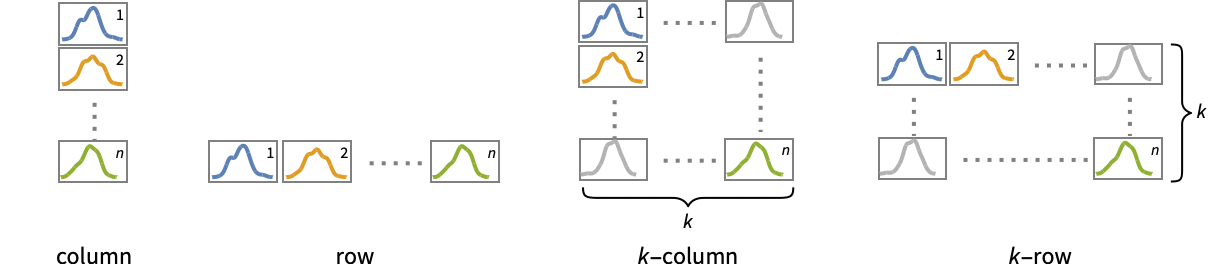
AspectRatio 1/GoldenRatio ratio of width to height Axes True whether to draw axes ClippingStyle None what to draw where curves are clipped ColorFunction Automatic how to determine the coloring of curves ColorFunctionScaling True whether to scale arguments to ColorFunction Filling None filling to insert under each curve FillingStyle Automatic style to use for filling MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh points to draw on each curve MeshFunctions {#1&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic methods to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for curves PlotPoints Automatic initial number of sample points PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotStyle Automatic graphics directives to specify the style for each object PlotTheme $PlotTheme overall theme for the plot RegionFunction (True&) how to determine whether a point should be included ScalingFunctions None how to scale individual coordinates WorkingPrecision MachinePrecision the precision used in internal computations for symbolic distributions - Possible settings for PlotLayout that show single curves in multiple plot panels include:
-
"Column" use separate curves in a column of panels "Row" use separate curves in a row of panels {"Column",k},{"Row",k} use k columns or rows {"Column",UpTo[k]},{"Row",UpTo[k]} use at most k columns or rows - The arguments supplied to RegionFunction, MeshFunctions, and ColorFunction are x and f, where f can be the PDF, CDF, etc. of the distribution.
- Possible highlighting effects for Highlighted and PlotHighlighting include:
-
style highlight the indicated curve 
"Ball" highlight and label the indicated point in a curve 
"Dropline" highlight and label the indicated point in a curve with droplines to the axes 
"XSlice" highlight and label all points along a vertical slice 
"YSlice" highlight and labels all points along a horizontal slice 
Placed[effect,pos] statically highlight the given position pos - Highlight position specifications pos include:
-
x,{x} effect at {x,y} with y chosen automatically {x,y} effect at {x,y} {pos1,pos2,…} multiple positions posi - With ScalingFunctions->{sx,sy}, the
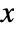 coordinate is scaled using sx and the
coordinate is scaled using sx and the 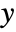 coordinate is scaled using sy.
coordinate is scaled using sy. -
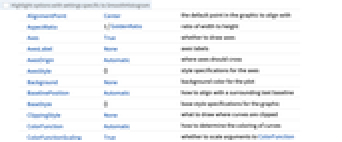
 Highlight options with settings specific to SmoothHistogram
Highlight options with settings specific to SmoothHistogram
-
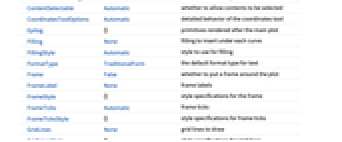
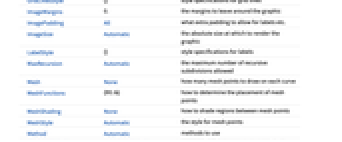
AlignmentPoint Center the default point in the graphic to align with AspectRatio 1/GoldenRatio ratio of width to height Axes True whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ClippingStyle None what to draw where curves are clipped ColorFunction Automatic how to determine the coloring of curves ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot Filling None filling to insert under each curve FillingStyle Automatic style to use for filling FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh None how many mesh points to draw on each curve MeshFunctions {#1&} how to determine the placement of mesh points MeshShading None how to shade regions between mesh points MeshStyle Automatic the style for mesh points Method Automatic methods to use PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotHighlighting Automatic highlighting effect for curves PlotLabel None an overall label for the plot PlotPoints Automatic initial number of sample points PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to specify the style for each object PlotTheme $PlotTheme overall theme for the plot PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RegionFunction (True&) how to determine whether a point should be included RotateLabel True whether to rotate y labels on the frame ScalingFunctions None how to scale individual coordinates Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks WorkingPrecision MachinePrecision the precision used in internal computations for symbolic distributions
List of all options
Examples
open all close allBasic Examples (3)
Scope (30)
Data (11)
Plot different distribution functions:
PlotRange is selected automatically:
Use PlotRange to focus on areas of interest:
Non-real data points are ignored:
Specify the number of times to refine the curve:
Override the default tooltips:
Use any object in the tooltip:
Use PopupWindow to provide additional drilldown information:
Numeric values in an association are used as the y coordinates:
Numeric keys and values in an association are used as the x and y coordinates:
The weights in WeightedData are ignored:
Tabular Data (1)
Bandwidth and Kernel (9)
Automatically select the bandwidth to use:
More data yields better approximations to the underlying distribution:
Explicitly specify the bandwidth:
Larger bandwidths yield smoother estimates:
Specify bandwidths in units of standard deviation:
Use bandwidths of ![]() and
and ![]() of the standard deviation:
of the standard deviation:
Allow bandwidth to vary adaptively with local density:
Vary the local sensitivity from ![]() (none) to
(none) to ![]() (full):
(full):
Vary the initial bandwidth for an adaptive estimate:
Specify an initial bandwidth of ![]() and
and ![]() respectively:
respectively:
Use any of several automatic bandwidth selection methods:
Silverman's method is used by default for bandwidth selection:
Options (79)
AspectRatio (4)
By default, SmoothHistogram uses a fixed height to width ratio for the plot:
Make the height the same as the width with AspectRatio1:
AspectRatioAutomatic determines the ratio from the plot ranges:
AspectRatioFull adjusts the height and width to tightly fit inside other constructs:
Axes (4)
Use AxesFalse to turn off axes:
Use AxesOrigin to specify where the axes intersect:
AxesLabel (4)
AxesOrigin (2)
AxesStyle (4)
ClippingStyle (4)
ColorFunction (5)
Color by scaled ![]() and
and ![]() coordinates:
coordinates:
Color with a named color scheme:
Fill with the color used for the curve:
ColorFunction has higher priority than PlotStyle for coloring the curve:
Use Automatic in MeshShading to use ColorFunction:
ColorFunctionScaling (2)
Filling (6)
FillingStyle (4)
Fill with red when the first curve is below the second, and blue when the second is below the first:
Use a variable filling style obtained from a ColorFunction:
ImageSize (7)
Use named sizes such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
MaxRecursion (2)
Each level of MaxRecursion will subdivide the initial mesh into a finer mesh:
Mesh (3)
MeshFunctions (2)
MeshShading (6)
Alternate red and blue segments of equal width in the ![]() direction:
direction:
Use None to remove segments:
MeshShading can be used with PlotStyle:
MeshShading has higher priority than PlotStyle for styling the curve:
Use PlotStyle for some segments by setting MeshShading to Automatic:
MeshShading can be used with ColorFunction:
MeshStyle (4)
PerformanceGoal (2)
PlotLayout (3)
PlotRange (2)
PlotRange is automatically calculated:
SmoothHistogram automatically chooses the plotting domain:
PlotStyle (6)
Use different style directives:
By default, different styles are chosen for multiple curves:
Explicitly specify the style for different curves:
PlotStyle can be combined with ColorFunction:
PlotStyle can be combined with MeshShading:
Applications (4)
The velocities in km/sec of 82 galaxies from six well-separated conic sections of an unfilled survey of the Corona Borealis region. Multimodality in such surveys is evidence for voids and superclusters in the far universe:
Multiple modes are readily detected for a variety of bandwidths:
Observe the density over many possible bandwidths and choose one that captures important features of the data while smoothing out noise. For presentation, it is best to choose a bandwidth that slightly undersmooths the data:
Choosing 6.0 seems to capture the important features of the snowfall data:
Visually compare data to a parametric model of its density:
Smooth histogram for the slice distribution of a random process:
Properties & Relations (5)
SmoothHistogram effectively plots the distribution function of SmoothKernelDistribution:
Use Histogram to plot the data in discrete bins:
Use SmoothDensityHistogram and SmoothHistogram3D for bivariate data:
Additional points will result in a better approximation of the underlying distribution:
As the bandwidth approaches infinity, the estimate approaches the shape of the kernel:
Possible Issues (1)
Using SmoothHistogram with multivariate data will plot multiple curves:
History
Introduced in 2010 (8.0) | Updated in 2014 (10.0) ▪ 2015 (10.2) ▪ 2021 (13.0) ▪ 2023 (13.3) ▪ 2025 (14.2)
Text
Wolfram Research (2010), SmoothHistogram, Wolfram Language function, https://reference.wolfram.com/language/ref/SmoothHistogram.html (updated 2025).
CMS
Wolfram Language. 2010. "SmoothHistogram." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/SmoothHistogram.html.
APA
Wolfram Language. (2010). SmoothHistogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SmoothHistogram.html
BibTeX
@misc{reference.wolfram_2025_smoothhistogram, author="Wolfram Research", title="{SmoothHistogram}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/SmoothHistogram.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_smoothhistogram, organization={Wolfram Research}, title={SmoothHistogram}, year={2025}, url={https://reference.wolfram.com/language/ref/SmoothHistogram.html}, note=[Accessed: 04-March-2026]}