DelaunayMesh
DelaunayMesh[{p1,p2,…}]
gives a MeshRegion representing the Delaunay mesh from the points p1, p2, ….
Details and Options

- DelaunayMesh is also known as Delaunay triangulation and Delaunay tetrahedralization.
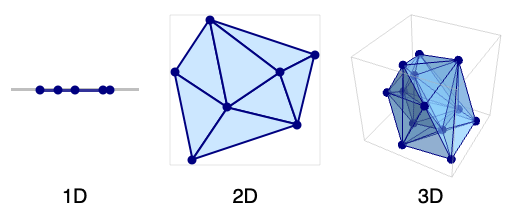
- A Delaunay mesh consists of intervals (in 1D), triangles (in 2D), tetrahedra (in 3D), and
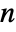 -dimensional simplices (in
-dimensional simplices (in 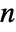 D).
D). - A Delaunay mesh has simplex cells defined by
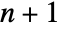 points, such that the circumsphere for the same
points, such that the circumsphere for the same 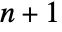 points contains no other points from the original points pi.
points contains no other points from the original points pi. - The Delaunay mesh gives a triangulation where the minimum interior angle is maximized.
- DelaunayMesh takes the same options as MeshRegion.
Examples
open allclose allBasic Examples (4)
Scope (3)
Create a 1D Delaunay mesh from a set of points:
Delaunay meshes are full dimensional:
Find its measure and centroid:
Find nearest distance and nearest point:
Create a 2D Delaunay mesh from a set of points:
Delaunay meshes are full dimensional:
Test for point membership or distance to the closest point in the region:
Create a 3D Delaunay mesh from a set of points:
Delaunay meshes are full dimensional:
Test for point membership or distance to the closest point in the region:
Options (11)
MeshCellHighlight (2)
MeshCellHighlight allows you to specify highlighting for parts of a DelaunayMesh:
MeshCellLabel (2)
MeshCellLabel can be used to label parts of a DelaunayMesh:
MeshCellMarker (1)
MeshCellMarker can be used to assign values to parts of a DelaunayMesh:
Use MeshCellLabel to show the markers:
MeshCellShapeFunction (2)
MeshCellShapeFunction allows you to specify functions for parts of a DelaunayMesh:
MeshCellStyle (2)
MeshCellStyle allows you to specify styling for parts of a DelaunayMesh:
Applications (5)
Generate lattice points of a 3D lattice basis:
Construct and visualize the mesh region:
Construct a 3D region from a point set:
Compare original region to Delaunay mesh:
Visualize the piecewise constant interpolation of city elevations in Colorado:
Voronoi mesh from city coordinates:
Create a function to map a given coordinate pair to the nearest known elevation:
Function to rescale elevation values to ![]() , suitable for color functions:
, suitable for color functions:
Piecewise constant contour plot of city elevations:
A similar plot can also be achieved with ListContourPlot:
Solve a PDE over a region defined by point set:
Create a mesh from selected points on a raster:
Function to convert a raster and a mesh region to polygons:
Properties & Relations (7)
The output of DelaunayMesh is always a full-dimensional MeshRegion:
DelaunayMesh consists of intervals in 1D:
The circumcircle for each triangle in a DelaunayMesh contains no other point:
Find circumcircles for all triangles:
Plot the circumcircles as disks:
The circumsphere for each tetrahedron in a DelaunayMesh contains no other point:
Find circumspheres for all tetrahedra:
ConvexHullMesh is effectively the BoundaryMesh of a DelaunayMesh:
Use TriangulateMesh to retriangulate a region:
VoronoiMesh is the dual of the DelaunayMesh:
Each Voronoi cell has a single point from the original point set:
Text
Wolfram Research (2014), DelaunayMesh, Wolfram Language function, https://reference.wolfram.com/language/ref/DelaunayMesh.html (updated 2015).
CMS
Wolfram Language. 2014. "DelaunayMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DelaunayMesh.html.
APA
Wolfram Language. (2014). DelaunayMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DelaunayMesh.html