DelaunayMesh

DelaunayMesh[{p1,p2,…}]

点 p1，p2，…からのドロネー(Delaunay)メッシュを表すMeshRegionを与える．

詳細とオプション

  • DelaunayMeshは，ドロネー三角形分割法およびドロネー四面体分割法としても知られている．
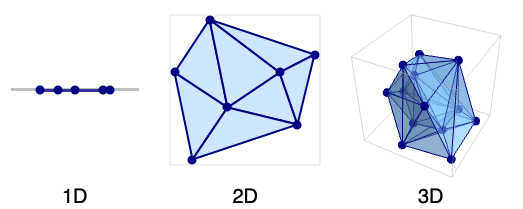
  • ドロネーメッシュは，1Dにおける区間，2Dにおける三角形，3Dにおける四面体， Dにおける 次元単体からなる．
  • ドロネーメッシュは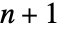，個の点で定義される単体セルを持つ．ただし，同じ 個の点の外接球はもとの点 piからの他のいかなる点も含んではならない，
  • ドロネーメッシュは，最小の内角が最大化されるような三角形分割を与える．
  • DelaunayMeshはMeshRegionと同じオプションを取る．

例題

すべて開くすべて閉じる

例  (4)

1Dドロネーメッシュ：

点のリストからの2Dドロネーメッシュ：

点のリストからの3Dドロネーメッシュ：

六方最密格子の最小ベクトルに対応する点からのドロネーメッシュ：

スコープ  (3)

点集合から1Dドロネーメッシュを作る：

基本特性：

ドロネーメッシュは全次元である：

ドロネーメッシュは有界である：

その測度と重心を求める：

最近距離と最近点を求める：

点集合から2Dドロネーメッシュを作る：

基本特性：

ドロネーメッシュは全次元である：

ドロネーメッシュは有界である：

その面積と重心を求める：

点の帰属あるいは領域内の最近点までの距離についての判定を行う：

点集合から3Dドロネーメッシュを作る：

基本特性：

ドロネーメッシュは全次元である：

ドロネーメッシュは有界である：

面積と重心を求める：

点の帰属あるいは領域内の最近点までの距離についての判定を行う：

オプション  (11)

MeshCellHighlight  (2)

MeshCellHighlightを使ってDelaunayMeshの一部のハイライトを指定することができる：

個々のセルは自身のセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

MeshCellLabel  (2)

MeshCellLabelを使ってDelaunayMeshの部分にラベルを付けることができる：

個々のセルには自身のセル指標を使ってラベルを付けることができる：

セルそれ自体を使うこともできる：

MeshCellMarker  (1)

MeshCellMarkerを使ってDelaunayMeshの一部に値を割り当てることができる：

MeshCellLabelを使ってマーカーを示す：

MeshCellShapeFunction  (2)

MeshCellShapeFunctionを使ってDelaunayMeshの部分のための関数を指定することができる：

個々のセルは自身のセル指標を使って描くことができる：

セルそれ自体を使うこともできる：

MeshCellStyle  (2)

MeshCellStyleを使ってDelaunayMeshの部分のスタイルを指定することができる：

個々のセルは自身のセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

PlotTheme  (2)

格子線と凡例のあるテーマを使う：

テーマを使ってワイヤーフレームを描く：

アプリケーション  (5)

3D格子基底の格子点を生成する：

メッシュ領域を構築し，可視化する：

点集合から3D領域を構築する：

もとの領域とドロネーメッシュを比較する：

コロラドにおける都市高度の区分的に一定な補間を可視化する：

都市の座標からのボロノイメッシュ：

指定された座標のペアを最も近い既知の高度にマップする関数を作成する：

高度値をに再スケールする関数．これは色関数に適している：

都市高度の区分的に一定な等高線プロット：

ListContourPlotを使っても同じようなプロットを得ることができる：

点集合で定義された領域上で偏微分方程式を解く：

ラスタ上の選ばれた点からメッシュを作る：

初期ロケータ点：

ラスタとメッシュ領域を多角形に変換する関数：

オーバーレイメッシュを作成する関数：

画像上でクリックを使い，ドラッグ可能な頂点を加えたり削除したりする：

特性と関係  (7)

DelaunayMeshの出力は，常に全次元のMeshRegionである：

DelaunayMeshは1Dにおける区間からなる：

2Dにおける三角形：

3Dにおける四面体：

DelaunayMesh中の各三角形の外接円は，他の点を含まない：

すべての三角形の外接円を求める：

外接円を円板としてプロットする：

DelaunayMesh中の各四面体の外接球は，他の点を含まない：

すべての四面体の外接球を求める：

外接球をプロットする：

ConvexHullMeshは，事実上，DelaunayMeshのBoundaryMeshである：

TriangulateMeshを使って領域を再度三角形分割する：

VoronoiMeshはDelaunayMeshの双対である：

各ボロノイセルは，もとの点集合の点を1つ含む：

Wolfram Research (2014), DelaunayMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/DelaunayMesh.html （2015年に更新）.

テキスト

Wolfram Research (2014), DelaunayMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/DelaunayMesh.html （2015年に更新）.

CMS

Wolfram Language. 2014. "DelaunayMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DelaunayMesh.html.

APA

Wolfram Language. (2014). DelaunayMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DelaunayMesh.html

BibTeX

@misc{reference.wolfram_2024_delaunaymesh, author="Wolfram Research", title="{DelaunayMesh}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DelaunayMesh.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_delaunaymesh, organization={Wolfram Research}, title={DelaunayMesh}, year={2015}, url={https://reference.wolfram.com/language/ref/DelaunayMesh.html}, note=[Accessed: 21-November-2024 ]}