DelaunayMesh
DelaunayMesh[{p1,p2,…}]
给出 MeshRegion 表示来自点 p1、p2、… 的德劳内网格.
更多信息和选项

- DelaunayMesh 也被称为德劳内三角和德劳内四面体.
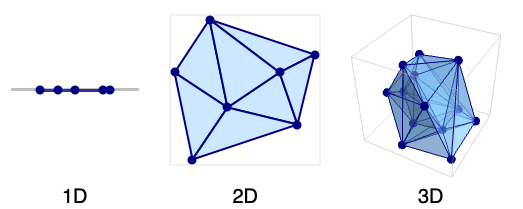
- 德劳内网格由区间(一维)、三角形(二维)、四面体(三维)和
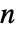 维单纯形(
维单纯形(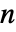 维)组成.
维)组成. - 德劳内网格具有的单纯形单元由
 个点定义,使得这相同的
个点定义,使得这相同的 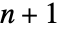 个点的外接圆不含有原始点 pi 中的其他点.
个点的外接圆不含有原始点 pi 中的其他点. - 德劳内网格给出一个三角化,其中最小内角最大化.
- DelaunayMesh 使用与 MeshRegion 相同的选项.
范例
打开所有单元关闭所有单元范围 (3)
选项 (11)
MeshCellHighlight (2)
MeshCellLabel (2)
MeshCellMarker (1)
MeshCellMarker 可用于对 DelaunayMesh 的部分赋值:
使用 MeshCellLabel 显示记号:
MeshCellShapeFunction (2)
MeshCellStyle (2)
应用 (5)
使用 ListContourPlot 也可以得到相似的图形:
属性和关系 (7)
DelaunayMesh 的输出总是全维的 MeshRegion:
DelaunayMesh 由一维区间组成:
DelaunayMesh 中每个三角形的外接圆都不含其他点:
DelaunayMesh 中每个四面体的外接圆都不含其他点:
ConvexHullMesh 实际上是 DelaunayMesh 的 BoundaryMesh:
使用 TriangulateMesh 对一个区域重新三角化:
VoronoiMesh 是 DelaunayMesh 的对偶:
文本
Wolfram Research (2014),DelaunayMesh,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DelaunayMesh.html (更新于 2015 年).
CMS
Wolfram 语言. 2014. "DelaunayMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2015. https://reference.wolfram.com/language/ref/DelaunayMesh.html.
APA
Wolfram 语言. (2014). DelaunayMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DelaunayMesh.html 年