WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

DerivativeFilter[data,{n1,n2,…}]

レベル i の data の ni次微分を計算する．

DerivativeFilter[data,{n1,n2,…},σ]

標準偏差 σ のガウススケールで微分を計算する．

DerivativeFilter[data,{der1,der2,…},…]

複数の微分 der1, der2, …を計算する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
データ  
パラメータ  
オプション  
InterpolationOrder  
Padding  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

DerivativeFilter

DerivativeFilter[data,{n1,n2,…}]

レベル i の data の ni次微分を計算する．

DerivativeFilter[data,{n1,n2,…},σ]

標準偏差 σ のガウススケールで微分を計算する．

DerivativeFilter[data,{der1,der2,…},…]

複数の微分 der1, der2, …を計算する．

詳細とオプション

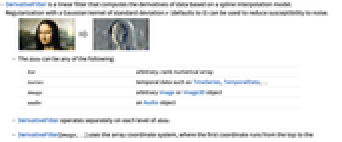
  • DerivativeFilterは，スプライン補間モデルに基づいてデータの微分を計算する線形フィルタである．標準偏差 σ（デフォルト値は0）のガウスカーネルによる正規化を使って，ノイズに対する感受性を削減することができる．
  • data は次のいずれでもよい．
  • list任意階数の数値配列
    tseriesTimeSeries，TemporalData等の時間データ
    image任意のImageオブジェクトまたはImage3Dオブジェクト
    audioAudioオブジェクト
    videoVideoオブジェクト
  • DerivativeFilterは data の各レベルに別々に動作する．
  • DerivativeFilter[image,…]は配列の座標系を使う．最初の座標は image の上から下へ，2番目の座標は左から右へ大きくなる．
  • DerivativeFilterは image と次元が等しい結果を与える．
  • DerivativeFilterには次のオプションを使うことができる．
  • InterpolationOrder Automatic補間次数（9まで）
    Padding "Fixed"充填法
  • Padding->{pad1,pad2,…}のときは，data の全次元に異なる充填スキームを使うことができる．
  • 微分次数は指定された補間次数よりも下でなければならない．

例題

すべて開く すべて閉じる

例  (3)

画像の水平微分：

画像の正規化された水平微分：

数値リストの微分：

スコープ  (14)

データ  (6)

2D配列の一次微分：

TimeSeriesオブジェクトの一次微分を得る：

Audio信号にフィルタをかける：

カラー画像の垂直微分：

動画のフレームにフィルタをかける：

3D画像の垂直微分：

パラメータ  (8)

リストの零次微分：

ステップ列の，一次，二次，三次微分：

画像の微分を可視化する：

水平微分：

両方の次元の二次微分：

ある画像について複数の微分を計算する：

3D画像の垂直微分：

水平微分のみ：

ガウス平滑化を使って微分を正規化する：

異なるガウススケールでの水平微分：

オプション  (3)

InterpolationOrder  (1)

InterpolationOrderの値を変えて配列にフィルタをかける：

Padding  (2)

異なる充填スキームを使った微分フィルタ：

異なる充填スキームを使ったグレースケール画像の一次微分：

各空間方向に異なる充填スキームを使う：

アプリケーション  (5)

画像の勾配を計算する：

画像のラプラシアンをスケール σ=6で計算する：

スケール σ=2でのリッジ検出：

T字路フィルタ：

カラー地図から州境を得る：

特性と関係  (4)

の値が大きいと，GaussianFilter とDerivativeFilterの結果は収束する：

スプライン補間のDerivativeFilterおよび関連微分は，同じ結果を返す：

補間関数の微分の上にフィルタの結果をプロットする：

バイナリ画像に微分フィルタを適用すると，実数型のグレースケール画像が返される：

DerivativeFilterは線形フィルタである：

Wolfram Research (2010), DerivativeFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/DerivativeFilter.html （2025年に更新）.

テキスト

Wolfram Research (2010), DerivativeFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/DerivativeFilter.html （2025年に更新）.

CMS

Wolfram Language. 2010. "DerivativeFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/DerivativeFilter.html.

APA

Wolfram Language. (2010). DerivativeFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DerivativeFilter.html

BibTeX

@misc{reference.wolfram_2025_derivativefilter, author="Wolfram Research", title="{DerivativeFilter}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/DerivativeFilter.html}", note=[Accessed: 18-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_derivativefilter, organization={Wolfram Research}, title={DerivativeFilter}, year={2025}, url={https://reference.wolfram.com/language/ref/DerivativeFilter.html}, note=[Accessed: 18-September-2025]}