RidgeFilter

RidgeFilter[data]

computes a measure for the presence of a ridge at every position of data.

RidgeFilter[data,σ]

uses the specified ridge scale σ.

Details and Options

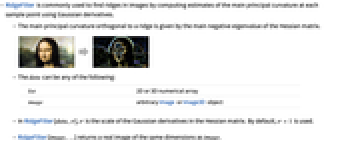
  • RidgeFilter is commonly used to find ridges in images by computing estimates of the main principal curvature at each sample point using Gaussian derivatives.
  • The main principal curvature orthogonal to a ridge is given by the main negative eigenvalue of the Hessian matrix.
  • The data can be any of the following:
  • list2D or 3D numerical array
    imagearbitrary Image or Image3D object
  • In RidgeFilter[data,σ], σ is the scale of the Gaussian derivatives in the Hessian matrix. By default, 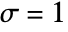is used.
  • RidgeFilter[image,…] returns a real image of the same dimensions as image.
  • RidgeFilter takes the following options used in the computation of the Hessian matrix:
  • InterpolationOrder Automaticinterpolation order
    Padding "Fixed"padding method
  • Possible settings for the InterpolationOrder option are 3, 4, 5, …, 9.
  • The Padding option accepts the settings "Fixed", "Periodic", "Reversed", "Reflected", or a numeric value. A list of two settings can specify different paddings for each dimension.

Examples

open allclose all

Basic Examples  (2)

Find the mountain ridges in a terrain elevation raster:

Sketch the thin parts in an engine block:

Scope  (4)

Data  (3)

Ridge filtering of a numeric matrix:

RidgeFilter of a grayscale image:

Use a ridge scale of 3:

RidgeFilter of a 3D image:

Parameters  (1)

By default, σ1 is used:

Use a larger σ for detecting thick lines:

Options  (2)

InterpolationOrder  (1)

Filtering an array using different InterpolationOrder values:

Padding  (1)

By default, a "Fixed" padding is used:

Specify a different padding:

Applications  (5)

Ridges in a two-dimensional array:

Enhance the strokes of handwritten characters:

Detect lines of a given width in a noisy image with uneven brightness:

Find the red ridges in a microscopic photo of a Yucca leaf:

Extract the walls:

Enhance trabecular bone structure:

Change the transfer function and background to further highlight the structure:

Properties & Relations  (2)

Ridge detection at scale σ=2 using DerivativeFilter:

Compare to the result of RidgeFilter:

Ridge filtering of an image gives a real-valued image:

Wolfram Research (2010), RidgeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/RidgeFilter.html (updated 2014).

Text

Wolfram Research (2010), RidgeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/RidgeFilter.html (updated 2014).

CMS

Wolfram Language. 2010. "RidgeFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/RidgeFilter.html.

APA

Wolfram Language. (2010). RidgeFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RidgeFilter.html

BibTeX

@misc{reference.wolfram_2024_ridgefilter, author="Wolfram Research", title="{RidgeFilter}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RidgeFilter.html}", note=[Accessed: 23-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ridgefilter, organization={Wolfram Research}, title={RidgeFilter}, year={2014}, url={https://reference.wolfram.com/language/ref/RidgeFilter.html}, note=[Accessed: 23-December-2024 ]}