RidgeFilter[data]
computes a measure for the presence of a ridge at every position of data.
RidgeFilter[data,σ]
uses the specified ridge scale σ.


RidgeFilter
RidgeFilter[data]
computes a measure for the presence of a ridge at every position of data.
RidgeFilter[data,σ]
uses the specified ridge scale σ.
Details and Options
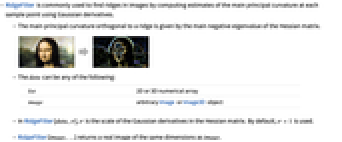
- RidgeFilter is commonly used to find ridges in images by computing estimates of the main principal curvature at each sample point using Gaussian derivatives.
- The main principal curvature orthogonal to a ridge is given by the main negative eigenvalue of the Hessian matrix.
- The data can be any of the following:
-
list 2D or 3D numerical array image arbitrary Image or Image3D object video a Video object - In RidgeFilter[data,σ], σ is the scale of the Gaussian derivatives in the Hessian matrix. By default,
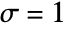 is used.
is used. - RidgeFilter[image,…] returns a real image of the same dimensions as image.
- RidgeFilter takes the following options used in the computation of the Hessian matrix:
-
InterpolationOrder Automatic interpolation order Padding "Fixed" padding method - Possible settings for the InterpolationOrder option are 3, 4, 5, …, 9.
- The Padding option accepts the settings "Fixed", "Periodic", "Reversed", "Reflected", or a numeric value. A list of two settings can specify different paddings for each dimension.

Examples
open all close allBasic Examples (2)
Scope (5)
Data (4)
Options (2)
InterpolationOrder (1)
Filtering an array using different InterpolationOrder values:
Applications (5)
Ridges in a two-dimensional array:
Enhance the strokes of handwritten characters:
Detect lines of a given width in a noisy image with uneven brightness:
Find the red ridges in a microscopic photo of a Yucca leaf:
Enhance trabecular bone structure:
Change the transfer function and background to further highlight the structure:
Properties & Relations (2)
Ridge detection at scale σ=2 using DerivativeFilter:
Compare to the result of RidgeFilter:
Text
Wolfram Research (2010), RidgeFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/RidgeFilter.html (updated 2025).
CMS
Wolfram Language. 2010. "RidgeFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/RidgeFilter.html.
APA
Wolfram Language. (2010). RidgeFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RidgeFilter.html
BibTeX
@misc{reference.wolfram_2025_ridgefilter, author="Wolfram Research", title="{RidgeFilter}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/RidgeFilter.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_ridgefilter, organization={Wolfram Research}, title={RidgeFilter}, year={2025}, url={https://reference.wolfram.com/language/ref/RidgeFilter.html}, note=[Accessed: 05-January-2026]}