DerivativeFilter

DerivativeFilter[data,{n1,n2,…}]

计算 data 在第 i 层的 ni 阶导数.

DerivativeFilter[data,{n1,n2,…},σ]

计算标准差为 σ 的高斯尺度上的导数.

DerivativeFilter[data,{der1,der2,…},…]

计算多个导数 der1、der2、….

更多信息和选项

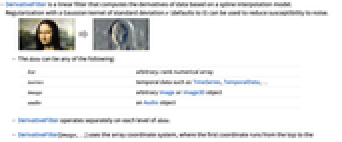
  • DerivativeFilter 是一个线性滤波器，根据样条插值模型计算数据的导数. 可以使用标准偏差为 σ （默认为 0）的高斯核的正则化来降低对噪声的敏感性.
  • data 可以为以下形式：
  • list任意阶数的数值数组
    tseries时态数据，如 TimeSeries、TemporalData、…
    image任意 Image 或 Image3D 对象
    audioAudio 对象
  • DerivativeFilter 分别对 data 的每一层进行运算.
  • DerivativeFilter[image,…] 使用数组坐标系统，其中第一个坐标从 image 的顶部到底部，第二个坐标从左到右增加.
  • DerivativeFilter 给出与 data 有同样维度的结果.
  • DerivativeFilter 可以采用下列选项：
  • InterpolationOrder Automatic插值阶数不高于 9
    Padding "Fixed"填充方法
  • 设置为 Padding->{pad1,pad2,…} 时，可以对 data 的不同维度使用不同的填充方案.
  • 导数的阶数必须小于指定的插值阶数.

范例

打开所有单元关闭所有单元

基本范例  (3)

图像的水平导数:

图像的正则化水平方向上的导数：

数值列表的导数：

范围  (13)

数据  (5)

二维数组的一阶导数：

获取 TimeSeries 对象的一阶导数：

对 Audio 信号进行滤波：

彩色图像在垂直方向上的导数：

三维图像在垂直方向上的导数：

参数  (8)

列表的零阶导数：

阶跃序列的第一、第二和第三阶导数：

图像在垂直方向上的导数：

水平方向上的导数：

两个维度上的二阶导数：

计算图像的几个导数：

三维图像在垂直方向上的导数：

水平方向上的导数：

用高斯平滑来规整导数：

不同高斯尺度下水平方向上的导数：

选项  (3)

InterpolationOrder  (1)

用不同的 InterpolationOrder 值来对数组滤波：

Padding  (2)

用不同的填充方案进行导数滤波：

用不同的填充方案对灰度图像进行一阶导数滤波：

在每个空间方向上使用不同的填充方案：

应用  (5)

计算图像的梯度：

计算标度 σ=6 的图像的拉普拉斯：

尺度 σ=2 时的脊探测：

T-junction 滤波:

从彩色地图中获取边界：

属性和关系  (4)

较大的情况下，GaussianFilter 和 DerivativeFilter 的结果收敛：

DerivativeFilter 和样条插值的相应导数返回相同的值：

将滤波器结果绘制在插值函数的导数的上方：

二进制图像的导数滤波给出了实数类型的灰度图像：

DerivativeFilter 是线性滤波器：

Wolfram Research (2010)，DerivativeFilter，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DerivativeFilter.html （更新于 2016 年）.

文本

Wolfram Research (2010)，DerivativeFilter，Wolfram 语言函数，https://reference.wolfram.com/language/ref/DerivativeFilter.html （更新于 2016 年）.

CMS

Wolfram 语言. 2010. "DerivativeFilter." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2016. https://reference.wolfram.com/language/ref/DerivativeFilter.html.

APA

Wolfram 语言. (2010). DerivativeFilter. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DerivativeFilter.html 年

BibTeX

@misc{reference.wolfram_2024_derivativefilter, author="Wolfram Research", title="{DerivativeFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/DerivativeFilter.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_derivativefilter, organization={Wolfram Research}, title={DerivativeFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/DerivativeFilter.html}, note=[Accessed: 17-November-2024 ]}