WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

DifferentialRoot[lde][x]

線形微分方程式 lde[h,x]で指定されるホロノミック関数 を与える．

DifferentialRoot[lde]

純粋なホロノミック関数 を表す．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
数値評価  
関数の特性  
微分  
積分  
級数展開  
一般化と拡張  
アプリケーション  
特性と関係  
考えられる問題  
おもしろい例題  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

DifferentialRoot

DifferentialRoot[lde][x]

線形微分方程式 lde[h,x]で指定されるホロノミック関数 を与える．

DifferentialRoot[lde]

純粋なホロノミック関数 を表す．

詳細

  • 記号操作・数値操作の両方に適した数学関数である．ホロノミック関数あるいはD有限関数としても知られている．
  • DifferentialRoot関数で定義されるホロノミック関数 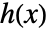は，多項式係数 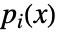，初期値 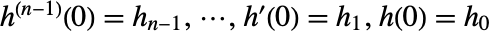のホロノミック微分方程式 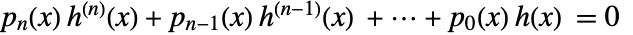を満足する．
  • DifferentialRootは，他の数学関数と同じように使うことができる．
  • FunctionExpandは，特殊関数を使ってDifferentialRoot関数を変換しようと試みる．
  • DifferentialRootで表される関数には，多くの特殊関数が含まれる．
  • DifferentialRootReduceは，ほとんどの特殊関数をDifferentialRootに変換することができる．
  • ホロノミック関数は，以下を含む多くの操作の下で閉じている．
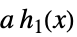  • , 定数倍，整数乗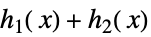
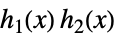
    , 和と積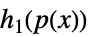
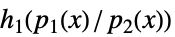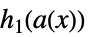
    , , 多項式，有理数，代数関数との組合せ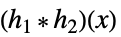
    たたみ込み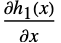
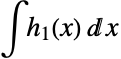
    , 導関数と積分
  • DifferentialRootは，Integrate，DSolve，GeneratingFunction等の関数によって，自動的に生成される．
  • Integrate，D，SeriesCoefficient，DSolve等の関数にはDifferentialRoot入力を使うことができる．
  • DifferentialRootは，任意の数値精度に評価することができる．
  • DifferentialRootは，自動的にリストに縫い込まれる．
  • DifferentialRoot[lde,pred]は，pred[z]で定義された（pred[z]は方程式と不等式を含むことができる）複素 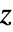平面上の分枝切断を避けるように限定された解を表す．

例題

すべて開く すべて閉じる

例  (2)

fが正弦関数となるように定義する：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {y''[x] + y[x] == 0, y[0] == 0, y'[0] == 1}]]

結果をプロットする：

Wolfram Language code: Plot[f[x], {x, 0, 2Pi}]

任意精度で数値的に評価する：

Wolfram Language code: f[N[1 + I, 30]]

結果を組込みのSin関数と比較する：

Wolfram Language code: Sin[N[1 + I, 30]]

微分方程式を解く：

Wolfram Language code: DSolve[y'''[x] - x^2 y'[x] - y[x] - Cos[x] == 0 && y[0] == 0 && y'[0] == 1 && y''[0] == 0, y, x]

数値：

Wolfram Language code: Table[y[n] /. First[%], {n, 1, 2, 0.2}]

スコープ  (23)

数値評価  (7)

機械精度で評価する：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'[x] - y[x] == 0, y[0] == 1}]][0.5]

高精度で評価する：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'[x] - y[x] == 0, y[0] == 1}]][1 / 2`50]

出力精度は入力精度に従う：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'[x] - y[x] == 0, y[0] == 1}]][0.10000000000000000001]

DifferentialRootは複素数のパラメータと引数を取る：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + y'[x] - y[x] == 0, y[1 / 2] == 1, y'[1 / 2] == -3 / 4}]][1 / 2 + 1.I]
Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + I y'[x] - y[x] == 0, y[1 / 2] == 1 + 4I, y'[1 / 2] == -3 / 4}]][1 / 2 + 1.I]

DifferentialRootは非厳密値入力パラメータを取る：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + y'[x] - y[x] == 0, y[1 / 2] == 1`20, y'[1 / 2] == -3 / 4}]][1 / 2 + 1I]
Wolfram Language code: Precision[%]

DifferentialRootを高精度で効率的に評価する：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + I y'[x] - y[x] == 0, y[1 / 2] == 1 + 4I, y'[1 / 2] == -3 / 4}]][2 / 10`100]//N//Timing

DifferentialRootは要素単位でリストと行列に縫い込まれる：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + I y'[x] - y[x] == 0, y[1 / 2] == 1 + 4I, y'[1 / 2] == -3 / 4}]][{0.2, 1.4}]
Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + I y'[x] - y[x] == 0, y[1 / 2] == 1 + 4I, y'[1 / 2] == -3 / 4}]][(| | | | :------- | :------- | | 3.1 | 1 / 3`20 | | 4 / 5`20 | 0.4 |)]

関数の特性  (5)

DifferentialRootオブジェクトは数学関数のすべての標準的な特徴を有している：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {y'''[x] + 2x y''[x] - y[x] == 0, y[1 / 2] == 1, y'[1 / 2] == -3 / 4, y''[1 / 2] == 0}]]

関数を積分する：

Wolfram Language code: Integrate[f[x], x]

それを微分する：

Wolfram Language code: D[f[x], x]

その級数展開を求める：

Wolfram Language code: Series[f[x], {x, 1 / 2, 3}]

実数上でプロットする：

Wolfram Language code: Plot[f[x], {x, -10, 10}]

複素平面上でプロットする：

Wolfram Language code: ComplexPlot[f[z], {z, 5}, RasterSize -> 50, PlotLegends -> Automatic]

サンプルの厳密値は自動的に生成される：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y''[x] + y[x] == 0, y[0] == 0, y'[0] == 1}]][Pi / 2]

FunctionExpandを使ってDifferentialRootオブジェクトを組込みの数学関数に変換しようとする：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y''[x] + y[x] == 0, y[0] == 0, y'[0] == 1}]][x]
Wolfram Language code: %//FunctionExpand

DifferentialRootは有理係数を持つ方程式に使うことができる：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'''[x] / x + y[x] == 0, y[0] == 0, y'[0] == 1, y''[0] == 0}]]

不均一なホロノミック方程式は，自動的に高次の均一な方程式に変換される：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'[x] - y[x] - Cos[x] == 0, y[0] == 1}]]

微分  (4)

DifferentialRootの導関数はDifferentialRoot関数である：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x + y[x] + y'[x] == 0, y[0] == 1}]][x]
Wolfram Language code: D[%, x]

DifferentialRootオブジェクトをパラメータについて微分する：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x + a y[x] + y'[x] == 0, y[0] == 1}]]
Wolfram Language code: D[f[x], a]

DifferentialRootオブジェクトの高次導関数を計算する：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x + a y[x] + y'[x] == 0, y[0] == 1}]][x]
Wolfram Language code: D[f, {x, 2}]
Wolfram Language code: D[f, x, a]
Wolfram Language code: D[f, {a, 2}]

DifferentialRootオブジェクトを微分する：

Wolfram Language code: df = D[DifferentialRoot[Function[{y, x}, {4x^2 - y[x] + y'[x] == 0, y[0] == 1}]][x], x]

の特定の値：

Wolfram Language code: df /. x -> RandomReal[{-5, 5}, 5]

のプロット：

Wolfram Language code: Plot[df, {x, -5, 5}]

積分  (4)

DifferentialRootオブジェクトの積分はDifferentialRootオブジェクトである：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x + y[x] + y'[x] == 0, y[0] == 1}]]
Wolfram Language code: Integrate[f[x], x]

DifferentialRootオブジェクトの高次積分を計算する：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x + a y[x] + y'[x] == 0, y[0] == 1}]][x]
Wolfram Language code: Integrate[f, x, x]

DifferentialRootオブジェクトの定積分を計算する：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x^2 + y[x] + y'[x] == 0, y[0] == 1}]]
Wolfram Language code: Subsuperscript[∫, -1, 1]f[x]ⅆx

DifferentialRootオブジェクトを積分する：

Wolfram Language code: F = Integrate[DifferentialRoot[Function[{y, x}, {x^2 + x y[x] + y'[x] == 0, y[0] == 1}]][x], x]

の特定の値：

Wolfram Language code: F /. x -> RandomReal[{-5, 5}, 5]

のプロット：

Wolfram Language code: Plot[F, {x, -5, 5}]

級数展開  (3)

DifferentialRootオブジェクトの級数展開を計算する：

Wolfram Language code: Series[DifferentialRoot[Function[{y, x}, {y''[x] + y[x] == 0, y[0] == 1, y'[0] == 1}]][x], {x, 0, 5}]

DifferentialRootオブジェクトのテイラー(Taylor)展開の 番目の係数を求める：

Wolfram Language code: SeriesCoefficient[DifferentialRoot[Function[{y, x}, {y''[x] + y[x] == 0, y[0] == 0, y'[0] == 1}]][x], {x, 0, n}]

最初の9個の係数を計算する：

Wolfram Language code: Table[%, {n, 0, 9}]

Sin関数の展開係数と比較する：

Wolfram Language code: CoefficientList[Series[Sin[x], {x, 0, 10}]//Normal, {x}]

DifferentialRootオブジェクトのパラメータを使った級数展開を計算する：

Wolfram Language code: Series[DifferentialRoot[Function[{y, x}, {y''[x] + a y[x] == 0, y[0] == 1, y'[0] == 1}]][x], {x, 0, 5}]

一般化と拡張  (1)

ホロノミックな定数項を持つ方程式は自動的に多項式係数に上げられる：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {y'[x] - y[x] - Cos[x] == 0, y[0] == 1}]]

アプリケーション  (4)

特殊関数からDifferentialRootオブジェクトを生成する：

Wolfram Language code: DifferentialRootReduce[BesselJ[2, Sqrt[x ^ 2 + 1]], x]

積分する：

Wolfram Language code: Integrate[%, x]

DifferentialRootオブジェクトは数学関数の標準的なあらゆる特徴を備えている：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {y'''[x] + 2x y''[x] - y[x] == 0, y[1 / 2] == 1, y'[1 / 2] == -3 / 4, y''[1 / 2] == 0}]][x]

DifferentialRootオブジェクトの級数展開の係数を求める：

Wolfram Language code: SeriesCoefficient[f, {x, 1 / 2, n}]

展開の最初の5つの係数を明示的に計算する：

Wolfram Language code: Table[%, {n, 0, 5}]

DifferentialRootオブジェクトの任意次数の導関数を計算する：

Wolfram Language code: df = D[f, x]
Wolfram Language code: D[f, {x, 4}]

DifferentialRootオブジェクトを積分する：

Wolfram Language code: F = Integrate[f, x]

f の積分である関数の微分方程式と初期条件を抽出する：

Wolfram Language code: %[[0, 1]][y, x]

関数 f，その積分と導関数をプロットする：

Wolfram Language code: Plot[{f, F, df}, {x, -10, 10}]

DifferentialRootを使って微分方程式を同次にする：

Wolfram Language code: dr = DifferentialRoot[Function[{y, x}, {y''[x] - x y[x] == Cos[x^2], y[0] == 1, y'[0] == -3 / 4 I}]]

同次方程式を抽出する：

Wolfram Language code: dr[[1]][y, x]

2つの数学関数の組合せであるDifferentialRootオブジェクトを生成する：

Wolfram Language code: DifferentialRootReduce[Sin[x] + 4 x Cos[x], x]

この関数が従う微分方程式と初期条件を抽出する：

Wolfram Language code: %[[0, 1]][y, x]

特性と関係  (5)

DifferentialRootReduceはDifferentialRootオブジェクトを生成する：

Wolfram Language code: DifferentialRootReduce[Cos[x], x]

DSolveは，解が既知の関数では得られない場合はDifferentialRootオブジェクトを生成する：

Wolfram Language code: DSolve[y'''[x] + y'[x] + x^3y[x] == 0, y[x], x]

GeneratingFunctionはDifferentialRootオブジェクトを生成することがある：

Wolfram Language code: GeneratingFunction[DifferenceRoot[Function[{y, n}, {y[n] + (1 + n) (2 + n) y[n + 2] == 0, y[0] == 0, y[1] == 1}]][n], n, x]

Integrateは，一般的なホロノミック関数に対してはDifferentialRootオブジェクトを返す：

Wolfram Language code: Integrate[DifferentialRoot[Function[{y, x}, {x + y[x] + y'[x] == 0, y[0] == 1}]][x], x]

Dは，一般的なホロノミック関数に対してはDifferentialRootオブジェクトを返す：

Wolfram Language code: D[DifferentialRoot[Function[{y, x}, {x + y[x] + y'[x] == 0, y[0] == 1}]][x], x]

考えられる問題  (3)

DifferentialRootは多項式係数を持つ線形微分方程式だけを取る：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {Sqrt[x]y''[x] - x y^2[x] == 0, y[0] == 1, y'[0] == -3 / 4 I}]][x]

DifferentialRootは初期値が特異点で与えられている場合は評価できない：

Wolfram Language code: DifferentialRoot[Function[{y, x}, {x y''[x] + y'[x] - y[x] == 0, y[0] == 1, y'[0] == -3 / 4 I}]][x]

組込み関数の分枝切断構造は自動計算された分枝切断構造とは異なることがある：

Wolfram Language code: f = DifferentialRoot[Function[{y, x}, {x (x - 1)y''[x] + ((1 + 1 / 2 + 1 / 3)x - 1 / 4)y'[x] + 1 / 2 * 1 / 3y[x] == 0, y[1 + I] == Hypergeometric2F1[1 / 2, 1 / 3, 1 / 4, 1 + I], y'[1 + I] == (D[Hypergeometric2F1[1 / 2, 1 / 3, 1 / 4, z], z] /. z -> 1 + I)}]]

複素平面上の領域によっては，f の値が対応する組込み関数の値とは異なることがある：

Wolfram Language code: f[2. - I]
Wolfram Language code: Hypergeometric2F1[1 / 2, 1 / 3, 1 / 4, 2. - I]

その他の領域については，DifferentialRootは同じ結果を与える：

Wolfram Language code: f[3. + 4I]
Wolfram Language code: Hypergeometric2F1[1 / 2, 1 / 3, 1 / 4, 3. + 4I]

おもしろい例題  (1)

既知の数学関数では解けない微分方程式を解く：

Wolfram Language code: sol = DSolveValue[{y''[x] + (x^10 - 1)y[x] == 0, y[0] == 1 / 2, y'[0] == -3 / 4}, y[x], x]

この解の数値を計算する：

Wolfram Language code: Table[sol, {x, 0., 1, 0.2}]

この解をプロットする：

Wolfram Language code: Plot[sol, {x, -3, 3}]

この解を微分する：

Wolfram Language code: dsol = D[sol, x]
Wolfram Research (2008), DifferentialRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferentialRoot.html （2020年に更新）.

テキスト

Wolfram Research (2008), DifferentialRoot, Wolfram言語関数， https://reference.wolfram.com/language/ref/DifferentialRoot.html （2020年に更新）.

CMS

Wolfram Language. 2008. "DifferentialRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/DifferentialRoot.html.

APA

Wolfram Language. (2008). DifferentialRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DifferentialRoot.html

BibTeX

@misc{reference.wolfram_2026_differentialroot, author="Wolfram Research", title="{DifferentialRoot}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/DifferentialRoot.html}", note=[Accessed: 27-September-2026]}

BibLaTeX

@online{reference.wolfram_2026_differentialroot, organization={Wolfram Research}, title={DifferentialRoot}, year={2020}, url={https://reference.wolfram.com/language/ref/DifferentialRoot.html}, note=[Accessed: 27-September-2026]}