DifferentialRoot
DifferentialRoot[lde][x]
给出由线性微分方程 lde[h,x] 指定的完整函数 ![]() .
.
DifferentialRoot[lde]
表示纯完整函数 ![]() .
.
更多信息

- 数学函数,适用于符号和数学运算;也称作完整函数和 D 有限函数.
- 由 DifferentialRoot 函数定义的完整函数
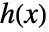 满足完整微分方程
满足完整微分方程 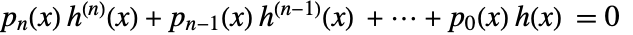 ,其中
,其中 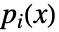 为多项式系数,初值为
为多项式系数,初值为 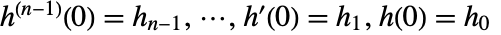 .
. - 可以和使用其它数学函数一样使用 DifferentialRoot.
- FunctionExpand 会试图转换 DifferentialRoot 函数, 用特殊函数来表示.
- 可以由 DifferentialRoot 表示的函数包括大量的特殊函数.
- DifferentialRootReduce 可以将大多数特殊函数转换为 DifferentialRoot 函数.
- 在许多运算中,完整序列是封闭的,其中包括:
-
 ,
, 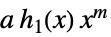
与常数相乘,整数幂 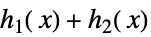 ,
, 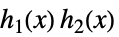
和与积 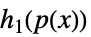 ,
, 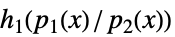 ,
, 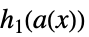
多项式函数、有理函数和代数函数的组合 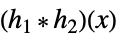
卷积 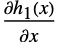 ,
, 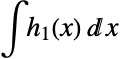
导数和积分 - DifferentialRoot 由诸如 Integrate、DSolve 和 GeneratingFunction 这样的函数自动产生.
- 诸如 Integrate、D、SeriesCoefficient 和 DSolve 这样的函数可使用 DifferentialRoot 输入.
- DifferentialRoot 可以计算出任意精度的结果.
- DifferentialRoot 自动逐项作用于列表.
- DifferentialRoot[lde,pred] 表示的解是受限的,以避免在由 pred[z] 定义的
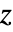 复平面中出现分割线,其中 pred[z] 可以包含等式和不等式.
复平面中出现分割线,其中 pred[z] 可以包含等式和不等式.
范例
打开所有单元关闭所有单元范围 (23)
数值计算 (7)
DifferentialRoot 使用复数的形式参数和实用参数:
DifferentialRoot 使用不精确的输入参数:
高效地在高精度下计算 DifferentialRoot:
DifferentialRoot 以元素方式线性作用于(threads over)列表和矩阵:
函数属性 (5)
DifferentialRoot 对象具有数学函数的所有标准特点:
使用 FunctionExpand 尝试将 DifferentialRoot 对象转换为一个内置数学函数:
DifferentialRoot 作用于有有理系数的方程:
微分 (4)
DifferentialRoot 的导数是一个 DifferentialRoot 函数:
求关于参数的 DifferentialRoot 对象的微分:
计算 DifferentialRoot 对象更高阶的导数:
求 DifferentialRoot 对象的微分:
积分 (4)
DifferentialRoot 对象的积分是一个 DifferentialRoot 对象:
计算 DifferentialRoot 对象的更高阶积分:
计算 DifferentialRoot 对象的定积分:
求 DifferentialRoot 对象的积分:
级数展开 (3)
计算 DifferentialRoot 对象的级数展开:
计算 DifferentialRoot 对象的泰勒展开式的第 ![]()
![]() 个系数:
个系数:
与 Sin 函数展开系数进行比较:
计算有一个参数的 DifferentialRoot 对象的级数展开:
应用 (4)
从特殊函数中生成 DifferentialRoot 对象:
DifferentialRoot 对象有数学函数的所有标准特点:
求 DifferentialRoot 对象的级数展开的系数:
计算 DifferentialRoot 对象的任意阶导数:
求 DifferentialRoot 对象的积分:
使用 DifferentialRoot 齐次化微分方程:
生成一个作为两个数学函数的组合的 DifferentialRoot 对象:
属性和关系 (5)
DifferentialRootReduce 生成 DifferentialRoot 对象:
若无法从已知函数中获取解,则 DSolve 生成一个 DifferentialRoot 对象:
GeneratingFunction 可能生成一个 DifferentialRoot 对象:
Integrate 为一般完全函数返回 DifferentialRoot 对象:
D 为一般完全函数返回 DifferentialRoot 对象:
可能存在的问题 (3)
DifferentialRoot 只接受有多项式系数的线性微分方程:
若给定的初始值为奇点,则 DifferentialRoot 不会计算:

对于复平面的一些区域而言,f 的值与其对应的内置函数值不同:
对于其他区域而言, DifferentialRoot 会给出同样的结果:
文本
Wolfram Research (2008),DifferentialRoot,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DifferentialRoot.html (更新于 2020 年).
CMS
Wolfram 语言. 2008. "DifferentialRoot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2020. https://reference.wolfram.com/language/ref/DifferentialRoot.html.
APA
Wolfram 语言. (2008). DifferentialRoot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DifferentialRoot.html 年