WOLFRAM

Wolfram Language & System Documentation Center

DiffusionPDETerm[vars]

モデル変数 vars の拡散項 を表す．

DiffusionPDETerm[vars,c]

拡散係数が の拡散項 を表す．

DiffusionPDETerm[vars,c,pars]

モデルパラメータ pars を使う．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
1D  
1D線対称  
2D  
Show More Show More
2D線対称  
3D  
連結  
連結線対称  
アプリケーション  
特性と関係  
考えられる問題  
関連項目
関連するガイド
履歴
引用書式

DiffusionPDETerm

DiffusionPDETerm[vars]

モデル変数 vars の拡散項 を表す．

DiffusionPDETerm[vars,c]

拡散係数が の拡散項 を表す．

DiffusionPDETerm[vars,c,pars]

モデルパラメータ pars を使う．

詳細

  • 拡散は物理学における中心概念で，熱力学，音響学，構造力学，流体力学等，数多くの分野で使われている．
  • 拡散は伝導としても知られている．
  • 拡散係数 がある拡散は，従属変数 の勾配のみに駆動される平衡過程である．
  • DiffusionPDETermは，偏微分方程式の一部として使われる微分演算子項を返す．
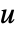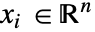  • DiffusionPDETermを使って，従属変数 ，独立変数 ，時間変数 の拡散方程式がモデル化できる．
  • 定常モデル変数 vars は vars={u[x1,…,xn],{x1,…,xn}}である．
  • 時間依存モデル変数 vars は vars={u[t,x1,…,xn],{x1,…,xn}}または vars={u[t,x1,…,xn],t,{x1,…,xn}}である．
  • 他のPDE項との関連における拡散項 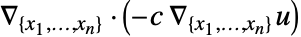は以下で与えられる．
  • 拡散の間，拡散が起こる媒体は静止したままであるのに対し，対流の場合は媒体が輸送機構となる．
  • 拡散係数 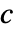は次の形を持つことができる．
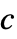
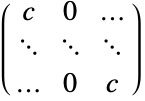
  • cスカラー 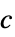，等方性拡散
    {c1,…,cn}
  • ベクトル 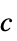，直交異方性拡散
    • {{c11,…,c1n},…,{cn1,…,cnn}}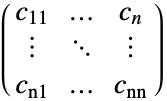
  • 行列 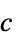，異方性拡散
  • 従属変数が{u1,…,um}の偏微分方程式系についての拡散は以下を表す．
  • PDE項の系との関連における拡散項．
  • 拡散係数 は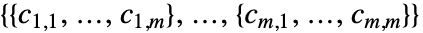の形の階数4のテンソルである．各部分行列 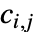は単一の従属変数と同じ方法で指定できる 行列である．
  • 記号拡散係数はMatrixSymbolで指定できる． »
  • 拡散係数 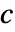は，時間，空間，パラメータ，従属変数に依存することがある．
  • 次は，使用可能なパラメータ pars である．
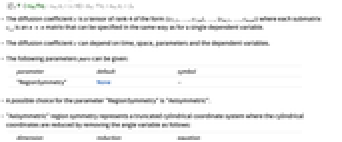
  • パラメータデフォルトシンボル
    "RegionSymmetry"None
  • パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある．
  • "Axisymmetric"領域対称性は，以下のように角度変数を削除することで円柱座標が縮小された，切り取られた円柱座標系を表す．
  • 次元縮小方程式
    1D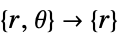
    2D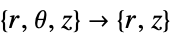
  • 係数 はNeumannValueの意味をもたらす．
  • 与えられた独立変数に明示的に依存しないすべての数量の偏導関数は0であるとみなされる．

例題

すべて開く すべて閉じる

例  (6)

定常拡散項を定義する：

項をアクティベートする：

パラメトリック拡散係数を置換して定常拡散項を定義する：

項をアクティブにする：

記号拡散項を定義する：

項をアクティブにする：

拡散項の固有値を求める：

基本項で構築されたポアソン(Poisson)方程式を構築し，記号的に解く：

ガウスの初期条件がある時間依存拡散方程式を解く：

初期条件が時間につれて平滑化される様子を可視化する：

曲線の下の面積が一定であることを確認する：

スコープ  (33)

1D  (6)

記号行列拡散項を定義する：

項をアクティブにする：

拡散項を指定しないと恒等行列係数になってしまう：

時間依存拡散項を定義する：

項をアクティブにする：

パラメトリック拡散係数を置き換えて定常拡散項を定義する：

項をアクティブにする：

固有値問題のモデル化にDiffusionPDETermを使う：

DiffusionPDETermを使って1Dポアソン方程式を設定する：

結果を可視化する：

1D線対称  (1)

1D軸対称拡散方程式を設定する：

これにActivateを適用する：

軸対称のケースは拡散方程式を構成する演算子を使って切り取られた円柱座標系を使った結果であることを確認する：

2D  (13)

2D定常拡散項を定義する：

項をアクティブにする：

拡散項を指定しないと恒等行列係数になってしまう：

2D定常拡散方程式を設定する：

項をアクティブにする：

記号行列拡散項を定義する：

項をアクティブにする：

2D時間依存拡散方程式を設定する：

項をアクティブにする：

拡散ベクトル係数で2D直交異方性の定常拡散項を定義する：

異方性拡散行列で2D定常拡散項を定義する：

異方性拡散行列で2D拡散項を定義する：

DiffusionPDETermを使って2Dポアソン方程式を設定する：

結果を可視化する：

基本的なPDE項からポアソン方程式を構築し，これを数値的に解く：

結果を可視化する：

方向の拡散定数の方が 方向よりも大きいベクトル値拡散係数を使う：

結果を可視化する：

方向の拡散定数の方が 方向よりも大きいベクトル値拡散係数を使う：

結果を可視化する：

異方性拡散係数を使う：

結果を可視化する：

2D線対称  (3)

2D軸対称性拡散方程式を設定する：

これにActivateを適用する：

軸対称性のケースは，拡散方程式を構成する演算子を使って切り取られた円柱座標系を使った結果であることを確認する：

2D軸対称拡散方程式を設定する：

これにActivateを適用する：

2D軸対称時間依存拡散方程式を設定する：

これにActivateを適用する：

3D  (1)

DiffusionPDETermを使って3Dポアソン方程式を設定する：

結果を可視化する：

連結  (6)

複数の従属変数がある拡散項を定義する：

複数の従属変数がある拡散項を定義する：

複数の従属変数と複数の拡散係数がある拡散項を定義する：

複数の従属変数と異方性拡散係数がある拡散項を定義する：

複数の従属変数とすべての係数が指定された拡散項を定義する：

非対角拡散係数は結合偏微分方程式においては可能である：

方程式を解く：

結果を可視化する：

連結線対称  (3)

DiffusionPDETermを使って複数の従属変数を持つ1D軸対称方程式を設定する：

境界条件を指定する：

方程式を数値的に解く：

同じ方程式を記号的に解く：

両結果の差を可視化する：

複数の従属変数を持つ軸対称拡散項を定義する：

これにActivateを適用する：

複数の従属変数と複数の拡散係数を持つ2D拡散軸対称項を定義する：

連立偏微分方程式を解く：

結果を可視化する：

アプリケーション  (9)

DiffusionPDETermを変数拡散係数と一緒に使う：

方程式を解く：

流束を計算する：

結果を可視化する：

DiffusionPDETermと軸対称幾何学を使って伝導性熱伝達をモデル化する．

分析領域は2D領域である．直交座標で完全な2D領域を定義する代りに，1Dの切取り円柱座標で領域を定義することができる．この系は 軸の周りで回転対称なので，円柱座標の変数 と は消失する．

方程式を設定する：

境界条件を指定する：

方程式を解く：

DSolveValueで記号的に解くこともできる：

結果間の差を可視化する：

DiffusionPDETermを使ってダムの下の種の拡散をモデル化する．領域を設定する：

モデルを設定する：

方程式を解く：

流束を計算する：

結果を可視化する：

ダムの下の種の濃度を求める．モデルを構築する：

方程式を解く：

種の濃度を可視化する：

ヘルムホルツ(Helmholtz)モデルを定義する：

ヘルムホルツ方程式の固有値について解く：

ソース項があるヘルムホルツ方程式を解く：

解を可視化する：

DiffusionPDETermと軸対称幾何学を使って伝導性熱伝達をモデル化する．分析領域は3Dの中空の円柱である．直交座標で完全な3D領域を定義する代りに，2Dの切取り円柱座標で領域を定義することができる．この系は 軸の周りで回転対称なので，円柱座標の変数 は消失する．

領域を設定する：

偏微分方程式モデルを設定する：

軸対称方程式を解く：

結果を可視化する：

円柱の一部について結果を3D空間で可視化する：

DiffusionPDETermと軸対称幾何学を使って非線形伝達性熱伝導をモデル化する．

領域を設定する：

空気の熱伝導率を求める：

偏微分方程式モデルを設定する：

方程式を解き，かかった時間とメモリを測定する：

軸対称の結果を可視化する：

計算にかかった合計時間と計算に使われたバイト数(MB)を出力する：

DiffusionPDETermを使って平面応力演算子を設定する：

モデルを設定する：

領域を設定する：

方程式を解く：

結果を可視化する：

流束を計算する：

ストークス(Stokes)流れのモデルを定義する：

方程式を設定する：

狭まる領域を定義する：

境界条件を設定する：

方程式を解く：

解を可視化する：

ストークス流れのモデルを拡張してナビエ(Navier)・ストークス流れのモデルにする．ストークス流れのモデルを定義する：

ナビエ・ストークス流れのモデルを定義する：

方程式を設定する：

領域を定義する：

境界条件を設定する：

方程式を解く：

解を可視化する：

特性と関係  (3)

異方性の拡散はと同じであることを確かめる：

2つの解には差がないことを可視化する：

ガウスの初期条件がある時間依存拡散方程式を解く：

解析的解は無限級数である：

Inactive和から数項取り出す：

数値解と解析的解の違いを可視化する：

DiffusionPDETermの平衡特性は，不連続初期条件平滑化に現れている：

不連続初期条件と初期条件の平滑化された進化を可視化する：

考えられる問題  (4)

演算子 中の負の符号は与える必要がない：

記号拡散係数は，スカラー係数と解釈される：

後続の置換でそれを考慮しなければならない：

項をアクティブにする：

数値拡散係数は，自動的に，適切な次元のIdentityMatrixと乗算される：

記号拡散係数を指定するよりよい方法はMatrixSymbolを使うことである：

MatrixSymbolを使うと演算子がアクティブにできる：

DiffusionPDETermは，ではなくをモデル化する：

解の差を可視化する：

Wolfram Research (2020), DiffusionPDETerm, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiffusionPDETerm.html （2025年に更新）.

テキスト

Wolfram Research (2020), DiffusionPDETerm, Wolfram言語関数， https://reference.wolfram.com/language/ref/DiffusionPDETerm.html （2025年に更新）.

CMS

Wolfram Language. 2020. "DiffusionPDETerm." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/DiffusionPDETerm.html.

APA

Wolfram Language. (2020). DiffusionPDETerm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiffusionPDETerm.html

BibTeX

@misc{reference.wolfram_2025_diffusionpdeterm, author="Wolfram Research", title="{DiffusionPDETerm}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}", note=[Accessed: 13-September-2025]}

BibLaTeX

@online{reference.wolfram_2025_diffusionpdeterm, organization={Wolfram Research}, title={DiffusionPDETerm}, year={2025}, url={https://reference.wolfram.com/language/ref/DiffusionPDETerm.html}, note=[Accessed: 13-September-2025]}