EllipticPi

EllipticPi[n,m]

gives the complete elliptic integral of the third kind TemplateBox[{n, m}, EllipticPi].

EllipticPi[n,ϕ,m]

gives the incomplete elliptic integral TemplateBox[{n, phi, m}, EllipticPi3].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For real 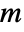, , 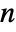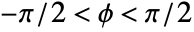and 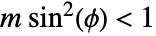, TemplateBox[{n, phi, m}, EllipticPi3]=int_0^phi(1-n sin^2(theta))^(-1)[1-m sin^2(theta)]^(-1/2)dtheta where the principal value integral is understood for .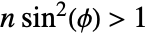
  • TemplateBox[{n, m}, EllipticPi]=TemplateBox[{n, {pi, /, 2}, m}, EllipticPi3].
  • EllipticPi[n,m] has branch cut discontinuities at 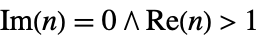and at .
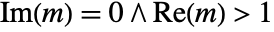  • EllipticPi[n,ϕ,m] has branch cut discontinuities 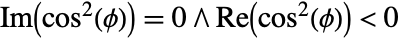at , at 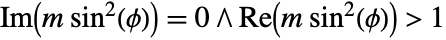and at .
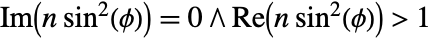  • For certain special arguments, EllipticPi automatically evaluates to exact values.
  • EllipticPi can be evaluated to arbitrary numerical precision.
  • EllipticPi automatically threads over lists.
  • EllipticPi can be used with Interval and CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (6)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Plot the incomplete elliptic integral over a subset of the complexes:

Series expansions at the origin:

Series expansion at Infinity:

Scope  (36)

Numerical Evaluation  (6)

Evaluate the incomplete elliptic integral numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate EllipticPi efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix EllipticPi function using MatrixFunction:

Specific Values  (3)

Simple exact values are generated automatically:

Values at infinity:

Find a real root of the equation TemplateBox[{x, {6, /, {(, 10, )}}}, EllipticPi]=3:

Visualization  (4)

Plot EllipticPi for various values of the second parameter :

Plot EllipticPi for various values of the first parameter :

Plot the incomplete elliptic integral TemplateBox[{n, {pi, /, 3}, m}, EllipticPi3] for various values of parameter :

Plot the real part of TemplateBox[{{-, 2}, z}, EllipticPi]:

Plot the imaginary part of TemplateBox[{{-, 2}, z}, EllipticPi]:

Function Properties  (9)

EllipticPi is not an analytic function:

Has both singularities and discontinuities:

EllipticPi is not a meromorphic function:

Real domain of TemplateBox[{n, {1, /, 5}}, EllipticPi]:

Real range of TemplateBox[{n, {1, /, 5}}, EllipticPi]:

Convert to a numerical approximation:

TemplateBox[{n, {1, /, 5}}, EllipticPi] is neither nondecreasing nor nonincreasing:

TemplateBox[{n, {1, /, 5}}, EllipticPi] is injective:

TemplateBox[{n, {1, /, 5}}, EllipticPi] is not surjective:

TemplateBox[{n, {1, /, 5}}, EllipticPi] is neither non-negative nor non-positive:

TemplateBox[{n, {1, /, 5}}, EllipticPi] is neither convex nor concave:

Differentiation  (4)

First derivative with respect to the first parameter:

Higher derivatives:

Plot higher derivatives for :

Differentiate with the respect to the second argument:

Higher derivatives:

Plot higher derivatives for :

Integration  (3)

Indefinite integral with respect to :

Definite integral:

Integral involving the incomplete elliptic integral:

Series Expansions  (3)

Taylor expansion for EllipticPi around :

Plot the first three approximations for TemplateBox[{{-, 2}, m}, EllipticPi] around :

Series expansion for EllipticPi around the branch point :

Plot the first three approximations for TemplateBox[{n, {-, 2}}, EllipticPi] around :

EllipticPi can be applied to power series:

Function Representations  (4)

Integral representation:

The complete elliptic integral of the third kind is a partial case of the incomplete elliptic integral:

EllipticPi can be represented as a DifferentialRoot:

TraditionalForm formatting:

Applications  (6)

Evaluate an elliptic integral:

Definition of the solid angle subtended by a disk (for instance a detector, a road sign) at the origin in the , ‐plane from a point :

Closed form result for the solid angle:

Numerical comparison:

Plot the solid angle as a function of horizontal distance and height:

This calculates the classical action for a relativistic 3D oscillator:

The action can be expressed using EllipticPi (for brevity, occurring roots are abbreviated):

A conformal map:

Visualize the image of lines of constant real and imaginary parts:

Parameterization of genus‐1 constant mean-curvature Wente torus:

Visualize 3‐lobe, 5‐lobe, 7‐lobe and 11‐lobe tori:

Numerically verify various change of parameter relations for EllipticPi:

Properties & Relations  (4)

EllipticPi[n,m] is real‐valued for and :

Expand special cases using assumptions:

This shows the branch cuts of the EllipticPi function:

Numerically find a root of a transcendental equation:

Possible Issues  (3)

Limits at branch cuts can be wrong:

The defining integral converges only under additional conditions:

Different argument conventions exist that result in modified results:

Wolfram Research (1988), EllipticPi, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticPi.html (updated 2022).

Text

Wolfram Research (1988), EllipticPi, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticPi.html (updated 2022).

CMS

Wolfram Language. 1988. "EllipticPi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticPi.html.

APA

Wolfram Language. (1988). EllipticPi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticPi.html

BibTeX

@misc{reference.wolfram_2024_ellipticpi, author="Wolfram Research", title="{EllipticPi}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticPi.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ellipticpi, organization={Wolfram Research}, title={EllipticPi}, year={2022}, url={https://reference.wolfram.com/language/ref/EllipticPi.html}, note=[Accessed: 21-December-2024 ]}