Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

EulerGamma

表示欧拉常数 γ，其数值 .

更多信息

数学常数，NumericQ 视为数字， D 视为常量.
EulerGamma 可以用 N 计算到任意数值精度.

背景

EulerGamma 是表示欧拉常数 γ 的符号，又被称为欧拉–马歇罗尼常数. EulerGamma 在数学中有许多等价的定义但最常见的定义还是包含了 HarmonicNumber[n] 和自然对数 Log[n] 的 $lim_(n->infty) (TemplateBox[{n}, HarmonicNumber]-log(n))$ 的极限值. EulerGamma 数值上 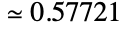. EulerGamma 出现在求和、求积、积分和求极限等各类数学计算中.
当 EulerGamma 作为符号时，它被当成精确值参与计算. 展开及化简一些复杂的含有 EulerGamma 的表达式可能要用到如 FunctionExpand 和 FullSimplify 这样的函数.
大多数数学家相信 EulerGamma 不仅是无理数（这意味着它不能被表示成任意一对整数的比值）也是超越数（这意味着它不是任何整数系数多项式的根）. 现在还不知道 EulerGamma 是否是某个进位制下的正规数（这意味着它在 b 进制下的各位数字均匀分布）. 除了出现在各种闭形式的求和与求积中之外，EulerGamma 还被推测不具备 Kontsevich–Zagier 周期（这意味着它不是任何定义在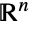上代数指定区域的单变量或多变量带有理系数的有理函数的绝对收敛积分的值）. 然而，所有上述猜想都尚未被证明或证否.
用 N 可以算出 EulerGamma 的任意精度的数值. 事实上在一台现代台式电脑上计算 EulerGamma 的前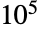位数字耗时都不到一秒. RealDigits 可用于返回 EulerGamma 的各位数字列表而 ContinuedFraction 则可得到其连分数展开的各项.
时的斯蒂尔吉斯常数 StieltjesGamma[n] 推广了 EulerGamma.

范例

打开所有单元关闭所有单元

基本范例 (1)

任意精度计算：

范围 (3)

执行一个数值计算：

求小数位数 10000 到 10050：

TraditionalForm 格式：

应用 (3)

γ 以 10 为基底的前20位数：

绘制成比除数的和：

计算渐近线的上限：

属性和关系 (2)

自动使用各种符号关系：

数学函数和运算通常包含 γ 的结果：

可能存在的问题 (1)

当前未知 EulerGamma 是否为一个代数数：

巧妙范例 (2)

连分数中的项：

包含 EulerGamma 的韦尔类型求和：

顶部