gives the Stieltjes constant ![]() .
.
StieltjesGamma[n,a]
gives the generalized Stieltjes constant ![]() .
.


StieltjesGamma
gives the Stieltjes constant ![]() .
.
StieltjesGamma[n,a]
gives the generalized Stieltjes constant ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
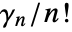 is the coefficient of
is the coefficient of 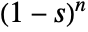 in the Laurent expansion of
in the Laurent expansion of 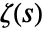 about the point
about the point 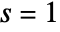 .
. - The
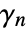 are generalizations of Euler's constant;
are generalizations of Euler's constant; 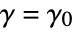 .
. 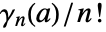 is the coefficient of
is the coefficient of  in the Laurent expansion of
in the Laurent expansion of 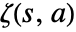 about the point
about the point 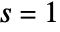 .
. - For certain special arguments, StieltjesGamma automatically evaluates to exact values.
- StieltjesGamma can be evaluated to arbitrary numerical precision.
- StieltjesGamma automatically threads over lists.
- StieltjesGamma can be used with Interval and CenteredInterval objects. »
Examples
open all close allBasic Examples (3)
Scope (5)
TraditionalForm formatting:
Evaluate for complex second argument:
The precision of the output tracks the precision of the input:
StieltjesGamma threads element-wise over lists:
StieltjesGamma can be used with Interval and CenteredInterval objects:
Applications (3)
Expansion of the Riemann zeta function:
Expansion of the Hurwitz zeta function:
Test Li’s criterion for the Riemann hypothesis:
All values should be positive:
Express integrals in terms of StieltjesGamma:
Properties & Relations (2)
Possible Issues (4)
Substitution of derivatives of Zeta at ![]() yields indeterminate values:
yields indeterminate values:
Use Limit to obtain the expansion coefficient:
The argument of StieltjesGamma must be an exact non-negative integer:
Use N to obtain a numerical approximation:
Alternatively, use two-argument form:
StieltjesGamma does not allow numericalization of its index:
It is currently not known if Stieltjes constants are algebraic numbers:
See Also
Related Guides
Related Links
History
Introduced in 1996 (3.0) | Updated in 2008 (7.0) ▪ 2021 (13.0) ▪ 2022 (13.1)
Text
Wolfram Research (1996), StieltjesGamma, Wolfram Language function, https://reference.wolfram.com/language/ref/StieltjesGamma.html (updated 2022).
CMS
Wolfram Language. 1996. "StieltjesGamma." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/StieltjesGamma.html.
APA
Wolfram Language. (1996). StieltjesGamma. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StieltjesGamma.html
BibTeX
@misc{reference.wolfram_2025_stieltjesgamma, author="Wolfram Research", title="{StieltjesGamma}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/StieltjesGamma.html}", note=[Accessed: 05-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_stieltjesgamma, organization={Wolfram Research}, title={StieltjesGamma}, year={2022}, url={https://reference.wolfram.com/language/ref/StieltjesGamma.html}, note=[Accessed: 05-January-2026]}