FindClique

FindClique[g]

グラフ g 中の最大クリークを求める．

FindClique[g,n]

最高で n 個の頂点を持つクリークを求める．

FindClique[g,{n}]

厳密に n 個の頂点を持つクリークを求める．

FindClique[g,{nmin,nmax}]

nminから nmaxまでの頂点を持つクリークを求める．

FindClique[g,nspec,s]

最高で s 個のクリークを求める．

FindClique[{g,v},…]

頂点 v のみを含むクリークを求める．

FindClique[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細

  • クリークとは対応する部分グラフが完全グラフとなる極大頂点集合である．
  • FindCliqueはクリークのリストを返す．
  • クリークが見付からなかった場合，FindCliqueは空のリストを返す．
  • FindClique[…,nspec,All]はすべてのクリークを求める．
  • 重み付きグラフの場合，FindCliqueは頂点重みの和が最大になる頂点集合を与える．
  • FindCliqueは，無向グラフ，有向グラフ，重み付きグラフ，多重グラフ，混合グラフに使うことができる．

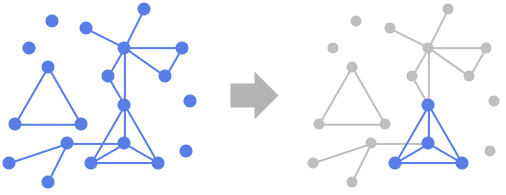
予備知識

  • FindCliqueは，頂点リストのリストとして返されたグラフ内の特定のサイズの最大クリーク集合を求める．ここでは，クリークは，対応する誘導された部分グラフが完全グラフであるような，頂点の部分集合である．クリークは，投影法の選択，パターンマッチング，金融，ネットワーク分析等に使用される．一般に，FindClique[g,nspec,s]は，グラフ g 内の指定されたサイズ nspec の s 個の最大クリークの集合を求める．
  • クリークには，最大と極大という重要な2つのタイプがある．両者は等しくない点に注意が必要である．最大クリークは，指定されたグラフの可能な最大数の頂点を含むクリークである．極大クリーク集合は，隣接頂点を1つ余計に含むことで拡大することができないクリーク，つまりより大きいクリークの部分集合ではないクリークのことである．したがって，（すでに最大サイズであれば拡張できないことは明らかなので）最大クリークは常に極大であるのに対し，逆は必ずしも真ではない．用語をさらに混同させるように，最大クリークを単に「クリーク」とする者もある．
  • FindCliqueはさまざまなサイズの極大クリークを求めることができる．FindCliqueは指定されたサイズの単一の極大クリーク，指定された数のクリーク，あるいはそのようなクリークすべてを求めることもできる．
  • FindClique[g]は，グラフ g の単一の最大クリークを求め，FindClique[g,Length/@FindClique[g],s]は最大 s 個の，FindClique[g,{Length[FindClique[g][[1]]},All]は，そのようなクリークすべてを求める．グラフ g の最大クリークのサイズはそのクリーク数として知られており，指定されたグラフの最大クリークの大きさを求める問題はNP完全，つまり計算が指数的に遅くなることになる．
  • FindClique[g,Infinity]はグラフ g の単一の極大クリークを求め，FindClique[g,Infinity,s]は最大 s 個の，FindClique[g,Infinity,All]はそのようなクリークすべてを求める．極大クリークは，グラフの色分けや非整数グラフの色分けを含むグラフ理論の応用において重要である．
  • 必ずしも極大ではないクリークはFindCliqueを使って直接求めることはできないが，すべての極大クリークのすべての部分集合の集合の和集合を取ることで単純化して列挙することができる．
  • グラフの（FindIndependentVertexSetで求めることができる）極大独立頂点集合は，そのGraphComplementの極大クリークに等しい．グラフ g の頂点の集合 vlist は，CompleteGraphQ[g,vlist]を使って（極大でもあるという条件なしに）クリークかどうかを調べることができる．FindKClique，FindKClan，FindKClubは，部分グラフ中で完全ではない連結を許すクリーク状の構造を求めることができる．

例題

すべて開くすべて閉じる

例  (2)

グラフ中の最大クリークを求める：

クリークを示す：

すべてのクリークを求める：

スコープ  (14)

指定  (8)

FindCliqueは無向グラフに使うことができる：

有向グラフ：

重み付きグラフ：

多重グラフ：

混合グラフ：

最大クリークを求める：

規則を使ってグラフを指定する：

FindCliqueは，大きいグラフに使うことができる：

一覧  (6)

厳密に3つの頂点を含むクリーク：

最大で2つの頂点を含むクリーク：

3つから5つまでの頂点を含むクリーク：

指定された頂点を含む最大クリーク：

グラフ中のすべてのクリークを求める：

クリークがない場合，FindCliqueは空リストを返す：

アプリケーション  (5)

グラフ中のすべてのクリークをハイライトする：

両親，兄弟，子どものように近い親族からなる家族のネットワーク中で，最大の近親家族を求める：

クリークをハイライトする：

Amazon.comで同じ買い手によってリンクされた本のネットワーク．「The Clinton Wars」と一緒に買われる本の最大のコレクションを求める：

1998年東アフリカ大使館攻撃のネットワークにおけるテロリストの下部組織を求める：

協力関係にあるテロリストの下部組織を示す：

ダエルエスサラームの攻撃セルを分離するために外部コンタクトを求める：

ダウ・ジョーンズ工業株平均の中で利益が同期して動きがちなものを求める：

まず，年初からの利益の相関を計算する：

選択した より高い相関係数を持つ株間に辺を描き，グラフを構築する：

同期して動くことが多い株の最大集合：

累積利益グラフを示す：

特性と関係  (8)

クリークは完全部分グラフを生成する極大頂点集合である：

{1,2,3}と{1,2,3,4}は完全部分グラフを生成するが極大ではない：

最大クリークは最も大きいクリークである：

クリークから帰納された部分グラフは完全グラフである：

グラフのクリークはその補グラフの独立頂点集合である：

グラフ内のクリークの頂点補集合はその補グラフの頂点被覆である：

完全グラフの最大クリークにはすべての頂点が含まれる：

完全 部ラフの最大クリークの大きさは である：

サイズ の最大クリークはコア構成要素に含まれる：

2コア構成要素：

のとき，すべてのクリークは クリーク， クラン， クラブ， プレックスである：

反対に，すべての1クリーク，1クラン，1クラブ，1プレックスはクリークである：

Wolfram Research (2010), FindClique, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindClique.html （2015年に更新）.

テキスト

Wolfram Research (2010), FindClique, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindClique.html （2015年に更新）.

CMS

Wolfram Language. 2010. "FindClique." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindClique.html.

APA

Wolfram Language. (2010). FindClique. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindClique.html

BibTeX

@misc{reference.wolfram_2024_findclique, author="Wolfram Research", title="{FindClique}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindClique.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findclique, organization={Wolfram Research}, title={FindClique}, year={2015}, url={https://reference.wolfram.com/language/ref/FindClique.html}, note=[Accessed: 21-November-2024 ]}