FindGraphIsomorphism

FindGraphIsomorphism[g1,g2]

頂点名を変えることでグラフ g1を g2にマップする同型写像を求める．

FindGraphIsomorphism[g1,g2,n]

最高で n 個の同型写像を求める．

FindGraphIsomorphism[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

  • FindGraphIsomorphismは辺保存全単射としても知られている．
  • FindGraphIsomorphismは，通常，同等の構造の識別とさまざまな表現の同等性の検証に使用される．
  • FindGraphIsomorphismは，wiと wjが g2中の隣接頂点なら viと vjが g1中の隣接頂点となり逆もまた真となるような連想のリストAssociation[v1->w1,v2->w2,…]を与える．
  • FindGraphIsomorphismは同型写像が求まらない場合には空リストを与える．
  • FindGraphIsomorphism[g1,g2,All]はすべての同型写像を与える．

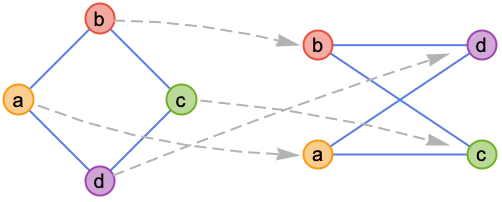
例題

すべて開くすべて閉じる

例  (2)

2つのグラフをマップする同型写像を求める：

すべての同形写像を求める：

スコープ  (8)

指定  (5)

FindGraphIsomorphismは無向グラフに使うことができる：

有向グラフ：

規則を使ってグラフを指定する：

同型写像が求まらない場合には空のリストが返される：

FindGraphIsomorphismは大きいグラフに使うことができる：

一覧表  (3)

2つのグラフをマップする同形写像を求める：

最高で2つの同形写像を求める：

すべての同形写像を求める：

アプリケーション  (1)

2つのグラフをマップする同型写像を求める：

マッピングに従って2つのグラフをハイライトし，ラベルを付ける：

特性と関係  (3)

同型グラフには同数の頂点と辺がある：

2つのグラフが同型写像かどうかIsomorphicGraphQを使って調べる：

同形写像のグラフは，同じ正準グラフを持つ：

Wolfram Research (2010), FindGraphIsomorphism, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html （2015年に更新）.

テキスト

Wolfram Research (2010), FindGraphIsomorphism, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html （2015年に更新）.

CMS

Wolfram Language. 2010. "FindGraphIsomorphism." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html.

APA

Wolfram Language. (2010). FindGraphIsomorphism. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html

BibTeX

@misc{reference.wolfram_2024_findgraphisomorphism, author="Wolfram Research", title="{FindGraphIsomorphism}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findgraphisomorphism, organization={Wolfram Research}, title={FindGraphIsomorphism}, year={2015}, url={https://reference.wolfram.com/language/ref/FindGraphIsomorphism.html}, note=[Accessed: 21-November-2024 ]}