FiniteFieldElementNorm

FiniteFieldElementNorm[a]

gives the absolute norm of the finite field element a.

FiniteFieldElementNorm[a,k]

gives the norm of a relative to the -element subfield of the ambient field of a.

FiniteFieldElementNorm[a,emb]

gives the norm of a relative to the finite field embedding emb.

Details

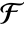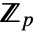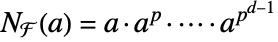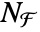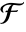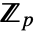  • For a finite field with characteristic p and extension degree d over , the absolute norm of a is given by . is a mapping from to and .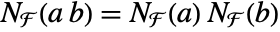
  • If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then .
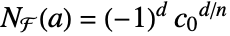  • FiniteFieldElementNorm[a] gives an integer between 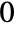and .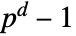
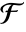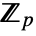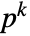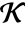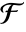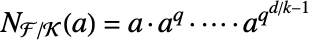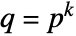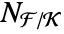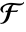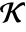  • For a finite field with characteristic p and extension degree d over , the norm of a relative to the -element subfield of is given by , where . is a mapping from to and 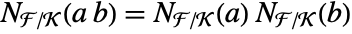. k needs to be a divisor of d.
  • If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then .
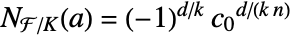  • FiniteFieldElementNorm[a,k] gives an element of .
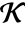  • If emb=FiniteFieldEmbedding[e1e2], then FiniteFieldElementNorm[a,emb] effectively gives emb["Projection"][FiniteFieldElementNorm[a,k]], where a belongs to the ambient field of e2 and k is the extension degree of the ambient field of e1.

Examples

open allclose all

Basic Examples  (1)

Represent a finite field with characteristic and extension degree :

Find the absolute norm of an element of the field:

Find the norm relative to the -element subfield:

Scope  (2)

Find the absolute norm of a finite field element:

The absolute norm given as a finite field element:

The norm relative to the -element subfield:

Compute the norm relative to a field embedding:

The result is equivalent to computing the norm relative to and projecting it to :

Applications  (1)

Define -linear mappings :

computes the determinant of :

Compute the determinant manually:

Properties & Relations  (7)

is a mapping from to which preserves multiplication:

The absolute norm of a is equal to the product of all conjugates of a:

Use FrobeniusAutomorphism to compute the conjugates of a:

The absolute norm of is equal to the absolute norm of :

If is the -element subfield of , then is a mapping from to , which preserves multiplication:

Use MinimalPolynomial to show that c and d belong to the -element subfield of :

This illustrates the multiplication-preserving property of :

Construct field embeddings such that :

FiniteFieldElementNorm satisfies a transitivity property:

If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then :

If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then :

Wolfram Research (2023), FiniteFieldElementNorm, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html.

Text

Wolfram Research (2023), FiniteFieldElementNorm, Wolfram Language function, https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html.

CMS

Wolfram Language. 2023. "FiniteFieldElementNorm." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html.

APA

Wolfram Language. (2023). FiniteFieldElementNorm. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html

BibTeX

@misc{reference.wolfram_2025_finitefieldelementnorm, author="Wolfram Research", title="{FiniteFieldElementNorm}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_finitefieldelementnorm, organization={Wolfram Research}, title={FiniteFieldElementNorm}, year={2023}, url={https://reference.wolfram.com/language/ref/FiniteFieldElementNorm.html}, note=[Accessed: 21-February-2025 ]}